В этом разделе описываются общие понятия, лежащие в основе библиотеки NumPy. Разница между копиями и представлениями при возвращении значений. Также рассмотрим механизм “broadcasting”, который неявно происходит во многих функциях NumPy.
Копии или представления объектов
Как вы могли заметить, при управлении массивом в NumPy можно возвращать его копию или представление. Но ни один из видов присваивания в NumPy не приводит к появлению копий самого массива или его элементов.
>>> a = np.array([1, 2, 3, 4])
>>> b = a
>>> b
array([1, 2, 3, 4])
>>> a[2] = 0
>>> b
array([1, 2, 0, 4])
Если присвоить один массив a переменной b, то это будет не операция копирования; массив b — это всего лишь еще один способ вызова a. Изменяя значение третьего элемента в a, вы изменяете его же и в b.
>>> c = a[0:2]
>>> c
array([1, 2])
>>> a[0] = 0
>>> c
array([0, 2])
Даже получая срез, вы все равно указываете на один и тот же массив. Если же нужно сгенерировать отдельный массив, необходимо использовать функцию copy().
>>> a = np.array([1, 2, 3, 4])
>>> c = a.copy()
>>> c
array([1, 2, 3, 4])
>>> a[0] = 0
>>> c
array([1, 2, 3, 4])
В этом случае даже при изменении объектов в массиве a, массив c будет оставаться неизменным.
Векторизация
Векторизация, как и транслирование, — это основа внутренней реализации NumPy. Векторизация — это отсутствие явного цикла при разработке кода. Самих циклов избежать не выйдет, но их внутренняя реализация заменяется на другие конструкции в коде. Приложение векторизации делает код более емким и читаемым. Можно сказать, что он становится более «Pythonic» внешне. Благодаря векторизации многие операции принимают более математический вид. Например, NumPy позволяет выражать умножение двух массивов вот так:
a * b
Или даже умножение двух матриц:
A * B
В других языках подобные операции выражаются за счет нескольких вложенных циклов и конструкции for. Например, так бы выглядела первая операция:
for (i = 0; i < rows; i++){
c[i] = a[i]*b[i];
}
А произведение матриц может быть выражено следующим образом:
for( i=0; i < rows; i++){
for(j=0; j < columns; j++){
c[i][j] = a[i][j]*b[i][j];
}
}
Использование NumPy делает код более читаемым и математическим.
Транслирование (Broadcasting)
Транслирование позволяет оператору или функции применяться по отношению к двум или большему количеству массивов, даже если они не одной формы. Тем не менее не все размерности поддаются транслированию; они должны соответствовать определенным правилам.
С помощью NumPy многомерные массивы можно классифицировать через форму (shape) — кортеж, каждый элемент которого представляет длину каждой размерности.
Транслирование может работать для двух массивов в том случае, если их размерности совместимы: их длина равна, или длина одной из них — 1. Если эти условия не соблюдены, возникает исключение, сообщающее, что два массива не совместимы.
>>> A = np.arange(16).reshape(4, 4)
>>> b = np.arange(4)
>>> A
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15]])
>>> b
array([0, 1, 2, 3])
В таком случае вы получаете два массива:
4 x 4
4
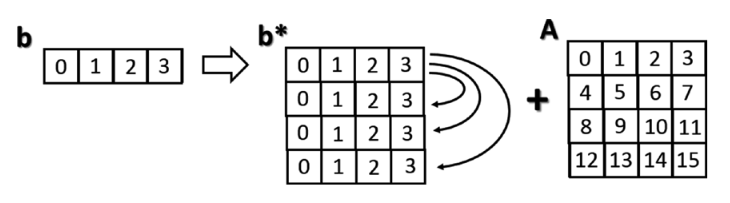
Есть два правила транслирования. В первую очередь нужно добавить 1 к каждой недостающей размерности. Если правила совместимости соблюдены, можно использовать транслирование и переходить ко второму правилу. Например:
4 x 4
4 x 1
Правило транслирования соблюдено. Можно переходить ко второму. Оно объясняет, как увеличить размер меньшего массива, чтобы он соответствовал большему, и можно было применить функцию или оператор поэлементно.
Второе правило предполагает, что недостающие элементы заполняются копиями заданных значений.
Когда у двух массивов одинаковые размерности, их значения можно суммировать.
>>> A + b
array([[ 0, 2, 4, 6],
[ 4, 6, 8, 10],
[ 8, 10, 12, 14],
[12, 14, 16, 18]])
Это простой случай, в котором один из массивов меньше второго. Могут быть и более сложные, когда у двух массивов разные размеры, и каждый меньше второго в конкретных размерностях.
>>> m = np.arange(6).reshape(3, 1, 2)
>>> n = np.arange(6).reshape(3, 2, 1)
>>> m
array([[[0, 1]],
[[2, 3]],
[[4, 5]]])
>>> n
array([[[0],
[1]],
[[2],
[3]],
[[4],
[5]]])
Даже в таком случае, анализируя форму двух массивов, можно увидеть, что они совместимы, а правила транслирования могут быть применены.
3 x 1 x 2
3 x 2 x 1
В этом случае размерности обоих массивов расширяются (транслирование).
m* = [[[0,1], n* = [[[0,0],
[0,1]], [1,1]],
[[2,3], [[2,2],
[2,3]], [3,3]],
[[4,5], [[4,4],
[4,5]]] [5,5]]]
Затем можно использовать, например, оператор сложения для двух массивов поэлементно.
>>> m + n
array([[[ 0, 1],
[ 1, 2]],
[[ 4, 5],
[ 5, 6]],
[[ 8, 9],
[ 9, 10]]])