Вы уже знаете, как создавать массив NumPy и как определять его элементы. Теперь пришло время разобраться с тем, как применять к ним различные операции.
Арифметические операторы
Арифметические операторы — первые, которые предстоит использовать. К числу наиболее очевидных относятся прибавление и умножение на скаляр.
>>> a = np.arange(4)
>>> a
array([0, 1, 2, 3])
>>> a+4
array([4, 5, 6, 7])
>>> a*2
array([0, 2, 4, 6])
Их можно использовать для двух массивов. В NumPy эти операции поэлементные, то есть, они применяются только к соответствующим друг другу элементам. Это должны быть объекты, которые занимают одно и то же положение, так что результатом станет новый массив, содержащий итоговые величины в тех же местах, что и операнды.
>>> b = np.arange(4,8)
>>> b
array([4, 5, 6, 7])
>>> a + b
array([ 4, 6, 8, 10])
>>> a – b
array([–4, –4, –4, –4])
>>> a * b
array([ 0, 5, 12, 21])
Более того, эти операторы доступны и для функций, если те возвращают массив NumPy. Например, можно перемножить массив на синус или квадратный корень элементов массива b.
>>> a * np.sin(b)
array([–0. , –0.95892427, –0.558831 , 1.9709598 ])
>>> a * np.sqrt(b)
array([ 0. , 2.23606798, 4.89897949, 7.93725393])
И даже в случае с многомерными массивами можно применять арифметические операторы поэлементно.
>>> A = np.arange(0, 9).reshape(3, 3)
>>> A
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
>>> B = np.ones((3, 3))
>>> B
array([[ 1., 1., 1.],
[ 1., 1., 1.],
[ 1., 1., 1.]])
>>> A * B
array([[ 0., 1., 2.],
[ 3., 4., 5.],
[ 6., 7., 8.]])
Произведение матриц
Выбор оператора для поэлементного применения — это странный аспект работы с библиотекой NumPy. В большинстве инструментов для анализа данных оператор * обозначает произведение матриц. Он применяется к обоим массивам. В NumPy же подобное произведение обозначается функцией dot(). Эта операция не поэлементная.
>>> np.dot(A,B)
array([[ 3., 3., 3.],
[ 12., 12., 12.],
[ 21., 21., 21.]])
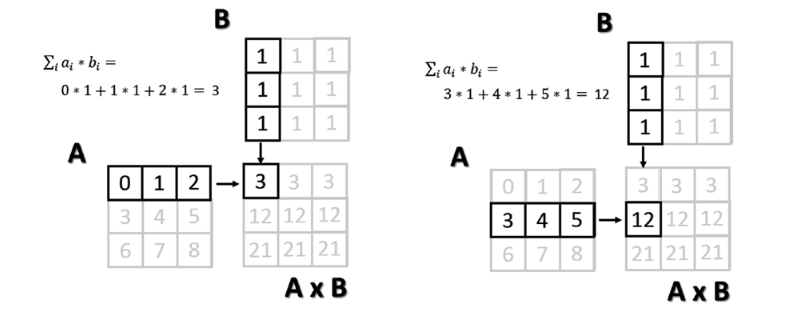
Каждый элемент результирующей матрицы — сумма произведений каждого элемента соответствующей строки в первой матрице с соответствующим элементом из колонки второй. Рисунок ниже показывает процесс произведения матриц (для двух элементов).
Еще один вариант записи произведения матриц — использование одной из двух матриц в качестве объекта функции dot().
>>> A.dot(B)
array([[ 3., 3., 3.],
[ 12., 12., 12.],
[ 21., 21., 21.]])
Но поскольку произведение матриц — это не коммутативная операция, порядок операндов имеет значение. В данном случае A*B не равняется B*A.
>>> np.dot(B,A)
array([[ 9., 12., 15.],
[ 9., 12., 15.],
[ 9., 12., 15.]])
Операторы инкремента и декремента
На самом деле, в Python таких операторов нет, поскольку нет операторов ++ или --. Для увеличения или уменьшения значения используются += и -=. Они не отличаются от предыдущих, но вместо создания нового массива с результатами присваивают новое значение тому же массиву.
>>> a = np.arange(4)
>>> a
array([0, 1, 2, 3])
>>> a += 1
>>> a
array([1, 2, 3, 4])
>>> a –= 1
>>> a
array([0, 1, 2, 3])
Таким образом использование этих операторов дает возможность получать более масштабные результаты, чем в случае с обычными операторами инкремента, увеличивающими значения на один. Их можно использовать в самых разных ситуациях. Например, они подходят для изменения значений без создания нового массива.
array([0, 1, 2, 3])
>>> a += 4
>>> a
array([4, 5, 6, 7])
>>> a *= 2
>>> a
array([ 8, 10, 12, 14])
Универсальные функции (ufunc)
Универсальная функция, известная также как ufunc, — это функция, которая применяется в массиве к каждому элементу. Это значит, что она воздействует на каждый элемент массива ввода, генерируя соответствующий результат в массив вывода. Финальный массив соответствует по размеру массиву ввода.
Под это определение подпадает множество математических и тригонометрических операций; например, вычисление квадратного корня с помощью sqrt(), логарифма с log() или синуса с sin().
>>> a = np.arange(1, 5)
>>> a
array([1, 2, 3, 4])
>>> np.sqrt(a)
array([ 1. , 1.41421356, 1.73205081, 2. ])
>>> np.log(a)
array([ 0. , 0.69314718, 1.09861229, 1.38629436])
>>> np.sin(a)
array([ 0.84147098, 0.90929743, 0.14112001, –0.7568025 ])
Многие функции уже реализованы в библиотеке NumPy.
Функции агрегации
Функции агрегации выполняют операцию на наборе значений, например, на массиве, и выдают один результат. Таким образом, сумма всех элементов массива — это результат работы функции агрегации. Многие из таких функций реализованы в классе ndarray.
>>> a = np.array([3.3, 4.5, 1.2, 5.7, 0.3])
>>> a.sum()
15.0
>>> a.min()
0.29999999999999999
>>> a.max()
5.7000000000000002
>>> a.mean()
3.0
>>> a.std()
2.0079840636817816