Помимо классических графиков, таких как столбчатые и круговые, можно представлять данные и другими способами. В интернете и разных источниках можно найти самые разные примеры визуализации данных, некоторые из которых выглядят невероятно. В этом разделе речь пойдет только о графических представлениях, но не о подробных способах их реализации. Можете считать это введением в мир визуализации данных.
Для выполнения кода импортируйте pyplot и numpy
import matplotlib.pyplot as plt import numpy as np
Контурные графики
В научном мире часто встречается тип контурных графиков или контурных карт. Они подходят для представления трехмерных поверхностей с помощью контурных карт, составленных из кривых, которые, в свою очередь, являются точками на поверхности на одном уровне (с одним и тем же значением z).
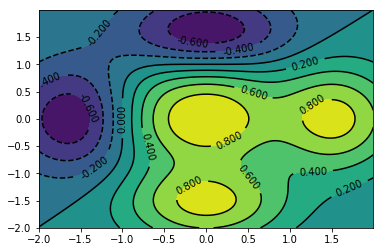
Хотя визуально контурный график — довольно сложная структура, ее реализация не так сложна, и все благодаря matplotlib. Во-первых, нужна функция z = f(x, y) для генерации трехмерной поверхности. Затем, имея значения x и y, определяющие площадь карты для вывода, можно вычислять значения z для каждой пары x и y с помощью функции f(x, y), которая и используется для этих целей. Наконец, благодаря функции contour() можно сгенерировать контурную карту на поверхности. Также часто требуется добавить цветную карту. Это площади, ограниченные кривыми уровней, заполненные цветным градиентом. Например, следующее изображения показывает отрицательные значения с помощью темных оттенков синего, а приближение к желтому и красному указывает на более высокие значения.
dx = 0.01; dy = 0.01
x = np.arange(-2.0,2.0,dx)
y = np.arange(-2.0,2.0,dy)
X,Y = np.meshgrid(x,y)
def f(x,y):
return (1 - y**5 + x**5)*np.exp(-x**2-y**2)
C = plt.contour(X,Y,f(X,Y),8,colors='black')
plt.contourf(X,Y,f(X,Y),8)
plt.clabel(C, inline=1, fontsize=10)
plt.show()
Это стандартный цветовой градиент. Но с помощью именованного аргумента cmap можно выбрать из большого число цветных карт.
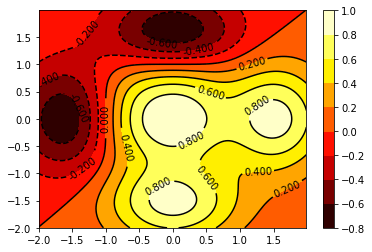
Более того при работе с таким визуальным представлением добавление градации цвета сторонам графа — это прямо необходимость. Для этого есть функция colorbar() в конце кода. В следующем изображении можно увидеть другой пример карты, которая начинается с черного, проходит через красный и затем превращается в желтый и белый на максимальных значениях. Это карта plt.cm.hot.
dx = 0.01; dy = 0.01
x = np.arange(-2.0,2.0,dx)
y = np.arange(-2.0,2.0,dy)
X,Y = np.meshgrid(x,y)
def f(x,y):
return (1 - y**5 + x**5)*np.exp(-x**2-y**2)
C = plt.contour(X,Y,f(X,Y),8,colors='black')
plt.contourf(X,Y,f(X,Y),8,cmap=plt.cm.hot)
plt.clabel(C, inline=1, fontsize=10)
plt.colorbar()
plt.show()
Лепестковые диаграммы
Еще один продвинутый тип диаграмм — лепестковые диаграммы. Он представляет собой набор круговых секторов, каждый из которых занимает определенный угол. Таким образом можно изобразить два значения, присвоив их величинам, обозначающим диаграмму: радиус r и угол θ. На самом деле, это полярные координаты — альтернативный способ представления функций на осях координат. С графической точки зрения такая диаграмма имеет свойства круговой и столбчатой. Как и в круговой диаграмме каждый сектор здесь указывает на значение в процентах по отношению к целому. Как и в столбчатой, расширение по радиусу — это числовое значение категории.
До сих пор в примерах использовался стандартный набор цветов, обозначаемых кодами (например, r — это красный). Однако есть возможность использовать любую последовательность цветов. Нужно лишь определить список строковых значений, содержащих RGB-коды в формате #rrggbb, которые будут соответствовать нужным цветам.
Странно, но для вывода лепестковой диаграммы нужно использовать функцию bar() и передать ей список углов θ и список радиальных расширений для каждого сектора.
N = 8
theta = np.arange(0.,2 * np.pi, 2 * np.pi / N)
radii = np.array([4,7,5,3,1,5,6,7])
plt.axes([0.025, 0.025, 0.95, 0.95], polar=True)
colors = np.array(['#4bb2c5','#c5b47f','#EAA228','#579575','#839557','#958c12','#953579','#4b5de4'])
bars = plt.bar(theta, radii, width=(2*np.pi/N), bottom=0.0, color=colors)
plt.show()
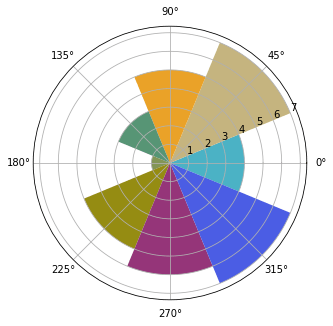
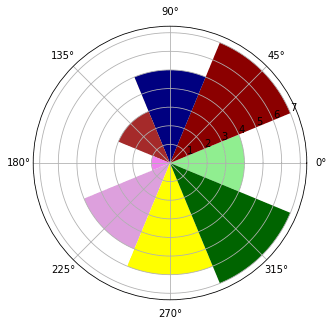
В этом примере определена последовательность цветов в формате #rrggbb, но ничто не мешает использовать строки с реальными названиями цветов.
N = 8
theta = np.arange(0.,2 * np.pi, 2 * np.pi / N)
radii = np.array([4,7,5,3,1,5,6,7])
plt.axes([0.025, 0.025, 0.95, 0.95], polar=True)
colors = np.array(['lightgreen','darkred','navy','brown','violet','plum','yellow','darkgreen'])
bars = plt.bar(theta, radii, width=(2*np.pi/N), bottom=0.0, color=colors)
plt.show()
Набор инструментов mplot3d
Набор mplot3d включен во все стандартные версии matplotlib и позволят расширить возможности создания трехмерных визуализаций данных. Если объект Figure выводится в отдельном окне, можно вращать оси трехмерного представления с помощью мыши.
Даже с этим пакетом продолжает использоваться объект Figure, но вместо объектов Axes определяется новый тип, Axes3D из этого набора. Поэтому нужно добавить один импорт в код.
from mpl_toolkits.mplot3d import Axes3D
Трехмерные поверхности
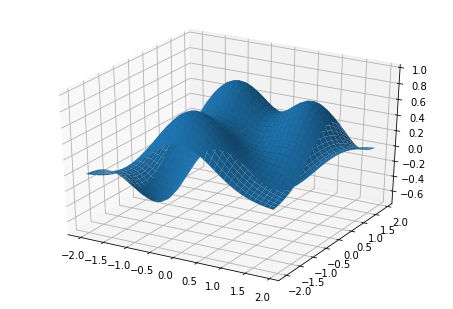
В прошлом разделе для представления трехмерных поверхностей использовался контурный график. Но с помощью mplot3D поверхности можно рисовать прямо в 3D. В этом примере используем ту же функцию z = f(x, y), что и в прошлом.
Когда meshgrid вычислена, можно вывести поверхность графика с помощью функции plot_surface().
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = Axes3D(fig)
X = np.arange(-2,2,0.1)
Y = np.arange(-2,2,0.1)
X,Y = np.meshgrid(X,Y)
def f(x,y):
return (1 - y**5 + x**5)*np.exp(-x**2-y**2)
ax.plot_surface(X,Y,f(X,Y), rstride=1, cstride=1)
plt.show()
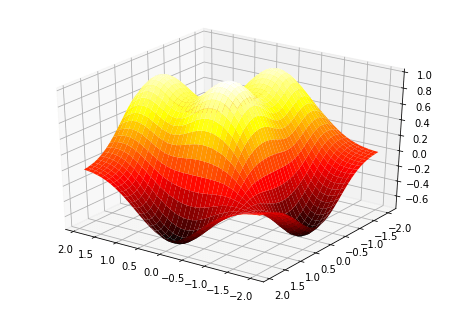
Трехмерная поверхность выделяется за счет изменения карты с помощью именованного аргумента cmap. Поверхность также можно вращать с помощью функции view_unit(). На самом деле, эта функция подстраивает точку обзора, откуда можно будет рассмотреть поверхность, изменяя аргументы elev и azim. С помощью их комбинирования можно получить поверхность, изображенную с любого угла. Первый аргумент настраивает высоту, а второй — угол поворота поверхности.
Например, можно поменять карту с помощью plt.cm.hot и повернуть угол на elev=30 и azim=125.
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = Axes3D(fig)
X = np.arange(-2,2,0.1)
Y = np.arange(-2,2,0.1)
X,Y = np.meshgrid(X,Y)
def f(x,y):
return (1 - y**5 + x**5)*np.exp(-x**2-y**2)
ax.plot_surface(X,Y,f(X,Y), rstride=1, cstride=1, cmap=plt.cm.hot)
ax.view_init(elev=30,azim=125)
plt.show()
Диаграмма рассеяния
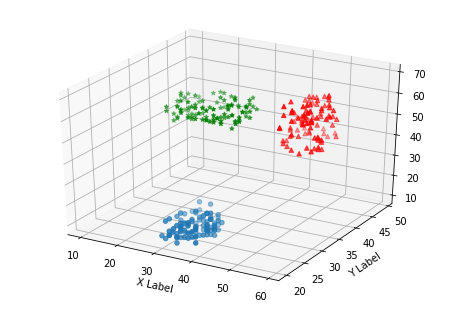
Самым используемым трехмерным графиком остается 3D график рассеяния. С его помощью можно определить, следуют ли точки определенным трендам и, что самое важное, скапливаются ли они.
В этом случае используется функция scatter() как и при построении обычного двумерного графика, но на объекте Axed3D. Таким образом можно визуализировать разные объекты Series, представленные через вызовы функции scatter() в единой трехмерной форме.
from mpl_toolkits.mplot3d import Axes3D
xs = np.random.randint(30,40,100)
ys = np.random.randint(20,30,100)
zs = np.random.randint(10,20,100)
xs2 = np.random.randint(50,60,100)
ys2 = np.random.randint(30,40,100)
zs2 = np.random.randint(50,70,100)
xs3 = np.random.randint(10,30,100)
ys3 = np.random.randint(40,50,100)
zs3 = np.random.randint(40,50,100)
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(xs,ys,zs)
ax.scatter(xs2,ys2,zs2,c='r',marker='^')
ax.scatter(xs3,ys3,zs3,c='g',marker='*')
ax.set_xlabel('X Label')
ax.set_ylabel('Y Label')
ax.set_xlabel('X Label')
plt.show()
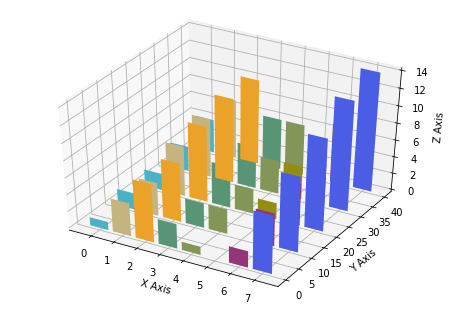
Столбчатые диаграммы в 3D
Также в анализе данных используются трехмерные столбчатые диаграммы. Здесь тоже нужно применять функцию bar() к объекту Axes3D. Если же определить несколько Series, то их можно накопить в нескольких вызовах функции bar() для одной 3D-визуализации.
from mpl_toolkits.mplot3d import Axes3D
x = np.arange(8)
y = np.random.randint(0,10,8)
y2 = y + np.random.randint(0,3,8)
y3 = y2 + np.random.randint(0,3,8)
y4 = y3 + np.random.randint(0,3,8)
y5 = y4 + np.random.randint(0,3,8)
clr = ['#4bb2c5','#c5b47f','#EAA228','#579575','#839557','#958c12','#953579','#4b5de4']
fig = plt.figure()
ax = Axes3D(fig)
ax.bar(x,y,0,zdir='y',color=clr)
ax.bar(x,y2,10,zdir='y',color=clr)
ax.bar(x,y3,20,zdir='y',color=clr)
ax.bar(x,y4,30,zdir='y',color=clr)
ax.bar(x,y5,40,zdir='y',color=clr)
ax.set_xlabel('X Axis')
ax.set_ylabel('Y Axis')
ax.set_zlabel('Z Axis')
ax.view_init(elev=40)
plt.show()
Многопанельные графики
Были рассмотрены самые разные способы представления данных на графике, в том числе и случаи, когда несколько наборов данных разделены в одном объекте Figure на нескольких подграфиках. В этом разделе речь пойдет о более сложных случаях.
Подграфики внутри графиков
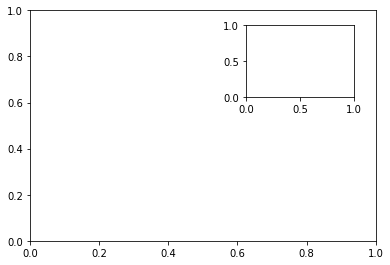
Есть возможность рассматривать графики внутри других ограниченных рамками. Поскольку речь идет о границах — объектах Axes — то есть необходимость разделять основные (основного графика) от тех, которые принадлежат добавляемому графику. Для этого используется функция figures(). С ее помощью нужно получить объект Figure, где будут определены два разных объекта Axes с помощью add_axes().
fig = plt.figure()
ax = fig.add_axes([0.1,0.1,0.8,0.8])
inner_ax = fig.add_axes([0.6,0.6,0.25,0.25])
plt.show()
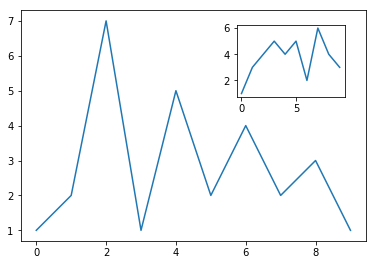
Чтобы лучше понять эффект этого режима, лучше заполнить предыдущий объект Axes с помощью реальных данных.
fig = plt.figure()
ax = fig.add_axes([0.1,0.1,0.8,0.8])
inner_ax = fig.add_axes([0.6,0.6,0.25,0.25])
x1 = np.arange(10)
y1 = np.array([1,2,7,1,5,2,4,2,3,1])
x2 = np.arange(10)
y2 = np.array([1,3,4,5,4,5,2,6,4,3])
ax.plot(x1,y1)
inner_ax.plot(x2,y2)
plt.show()
Сетка подграфиков
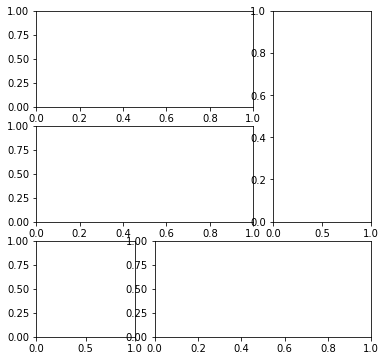
Есть другой способ создания подграфиков. С помощью функции subplots() их нужно добавить, разбив таким образом график на секторы. matplotlib позволяет работать даже с более сложными случаями с помощью функции GridSpec(). Это подразделение позволяет разбить область на сетку подграфиков, каждому из которых можно присвоить свой график, так что результатом будет сетка с подграфиками разных размеров с разными направлениями.
gs = plt.GridSpec(3,3)
fig = plt.figure(figsize=(6,6))
fig.add_subplot(gs[1,:2])
fig.add_subplot(gs[0,:2])
fig.add_subplot(gs[2,0])
fig.add_subplot(gs[:2,2])
fig.add_subplot(gs[2,1:])
plt.show()
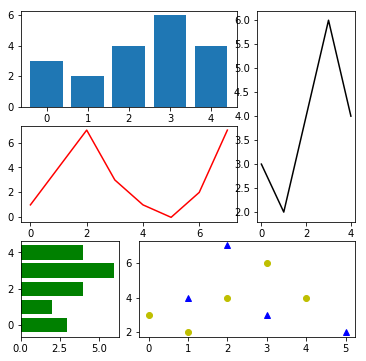
Создать такую сетку несложно. Осталось разобраться, как заполнить ее данными. Для этого нужно использовать объект Axes, который возвращает каждая функция add_subplot(). В конце остается вызвать plot() для вывода конкретного графика.
gs = plt.GridSpec(3,3)
fig = plt.figure(figsize=(6,6))
x1 = np.array([1,3,2,5])
y1 = np.array([4,3,7,2])
x2 = np.arange(5)
y2 = np.array([3,2,4,6,4])
s1 = fig.add_subplot(gs[1,:2])
s1.plot(x,y,'r')
s2 = fig.add_subplot(gs[0,:2])
s2.bar(x2,y2)
s3 = fig.add_subplot(gs[2,0])
s3.barh(x2,y2,color='g')
s4 = fig.add_subplot(gs[:2,2])
s4.plot(x2,y2,'k')
s5 = fig.add_subplot(gs[2,1:])
s5.plot(x1,y1,'b^',x2,y2,'yo')
plt.show()