В компьютерном зрении обнаружение объекта — это проблема определения местоположения одного или нескольких объектов на изображении. Помимо традиционных методов обнаружения, продвинутые модели глубокого обучения, такие как R-CNN и YOLO, могут обеспечить впечатляющие результаты при различных типах объектов. Эти модели принимают изображение в качестве входных данных и возвращают координаты прямоугольника, ограничивающего пространство вокруг каждого найденного объекта.
В этом руководстве обсуждается матрица ошибок и то, как рассчитываются precision, recall и accuracy метрики.
Здесь мы рассмотрим:
- Матрицу ошибок для двоичной классификации.
- Матрицу ошибок для мультиклассовой классификации.
- Расчет матрицы ошибок с помощью Scikit-learn.
- Accuracy, Precision и Recall.
- Precision или Recall?
Матрица ошибок для бинарной классификации
В бинарной классификации каждая выборка относится к одному из двух классов. Обычно им присваиваются такие метки, как 1 и 0, или положительный и отрицательный (Positive и Negative). Также могут использоваться более конкретные обозначения для классов: злокачественный или доброкачественный (например, если проблема связана с классификацией рака), успех или неудача (если речь идет о классификации результатов тестов учащихся).
Предположим, что существует проблема бинарной классификации с классами positive и negative. Вот пример достоверных или эталонных меток для семи выборок, используемых для обучения модели.
positive, negative, negative, positive, positive, positive, negativeТакие наименования нужны в первую очередь для того, чтобы нам, людям, было проще различать классы. Для модели более важна числовая оценка. Обычно при передаче очередного набора данных на выходе вы получите не метку класса, а числовой результат. Например, когда эти семь семплов вводятся в модель, каждому классу будут назначены следующие значения:
0.6, 0.2, 0.55, 0.9, 0.4, 0.8, 0.5На основании полученных оценок каждой выборке присваивается соответствующий класс. Такое преобразование числовых результатов в метки происходит с помощью порогового значения. Данное граничное условие является гиперпараметром модели и может быть определено пользователем. Например, если порог равен 0.5, тогда любая оценка, которая больше или равна 0.5, получает положительную метку. В противном случае — отрицательную. Вот предсказанные алгоритмом классы:
positive (0.6), negative (0.2), positive (0.55), positive (0.9), negative (0.4), positive (0.8), positive (0.5)Сравните достоверные и полученные метки — мы имеем 4 верных и 3 неверных предсказания. Стоит добавить, что изменение граничного условия отражается на результатах. Например, установка порога, равного 0.6, оставляет только два неверных прогноза.
Реальность: positive, negative, negative, positive, positive, positive, negative
Предсказания: positive, negative, positive, positive, negative, positive, positiveДля получения дополнительной информации о характеристиках модели используется матрица ошибок (confusion matrix). Матрица ошибок помогает нам визуализировать, «ошиблась» ли модель при различении двух классов. Как видно на следующем рисунке, это матрица 2х2. Названия строк представляют собой эталонные метки, а названия столбцов — предсказанные.
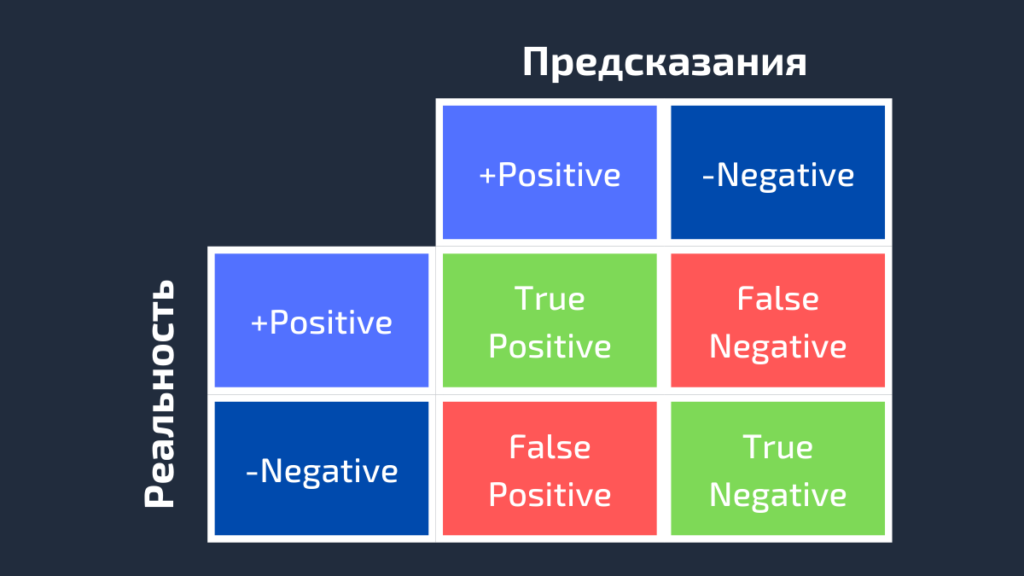
Четыре элемента матрицы (клетки красного и зеленого цвета) представляют собой четыре метрики, которые подсчитывают количество правильных и неправильных прогнозов, сделанных моделью. Каждому элементу дается метка, состоящая из двух слов:
- True или False.
- Positive или Negative.
True, если получено верное предсказание, то есть эталонные и предсказанные метки классов совпадают, и False, когда они не совпадают. Positive или Negative — названия предсказанных меток.
Таким образом, всякий раз, когда прогноз неверен, первое слово в ячейке False, когда верен — True. Наша цель состоит в том, чтобы максимизировать показатели со словом «True» (True Positive и True Negative) и минимизировать два других (False Positive и False Negative). Четыре метрики в матрице ошибок представляют собой следующее:
- Верхний левый элемент (True Positive): сколько раз модель правильно классифицировала Positive как Positive?
- Верхний правый (False Negative): сколько раз модель неправильно классифицировала Positive как Negative?
- Нижний левый (False Positive): сколько раз модель неправильно классифицировала Negative как Positive?
- Нижний правый (True Negative): сколько раз модель правильно классифицировала Negative как Negative?
Мы можем рассчитать эти четыре показателя для семи предсказаний, использованных нами ранее. Полученная матрица ошибок представлена на следующем рисунке.
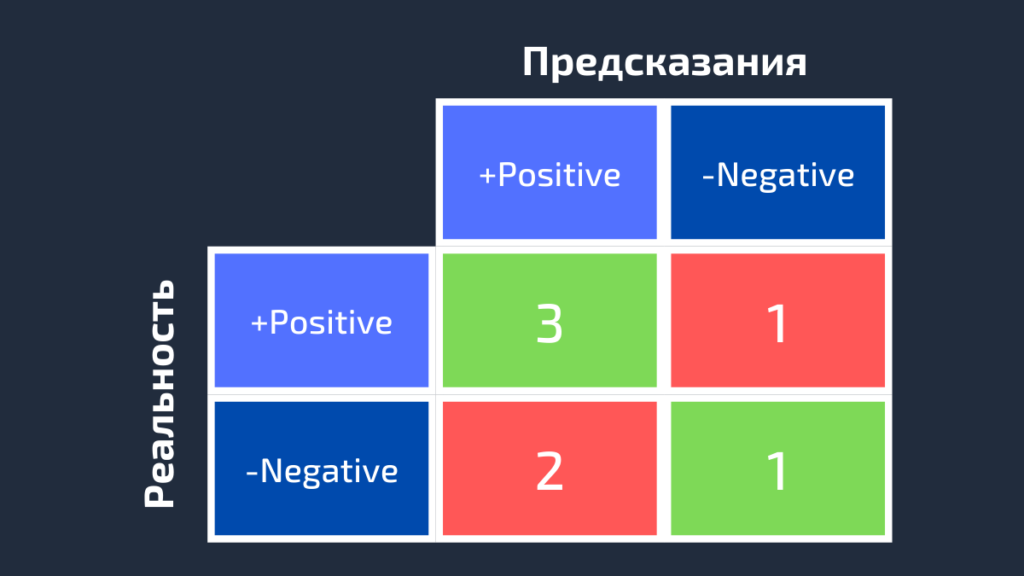
Вот так вычисляется матрица ошибок для задачи двоичной классификации. Теперь посмотрим, как решить данную проблему для большего числа классов.
Матрица ошибок для мультиклассовой классификации
Что, если у нас более двух классов? Как вычислить эти четыре метрики в матрице ошибок для задачи мультиклассовой классификации? Очень просто!
Предположим, имеется 9 семплов, каждый из которых относится к одному из трех классов: White, Black или Red. Вот достоверные метки для 9 выборок:
Red, Black, Red, White, White, Red, Black, Red, WhiteПосле загрузки данных модель делает следующее предсказание:
Red, White, Black, White, Red, Red, Black, White, RedДля удобства сравнения здесь они расположены рядом.
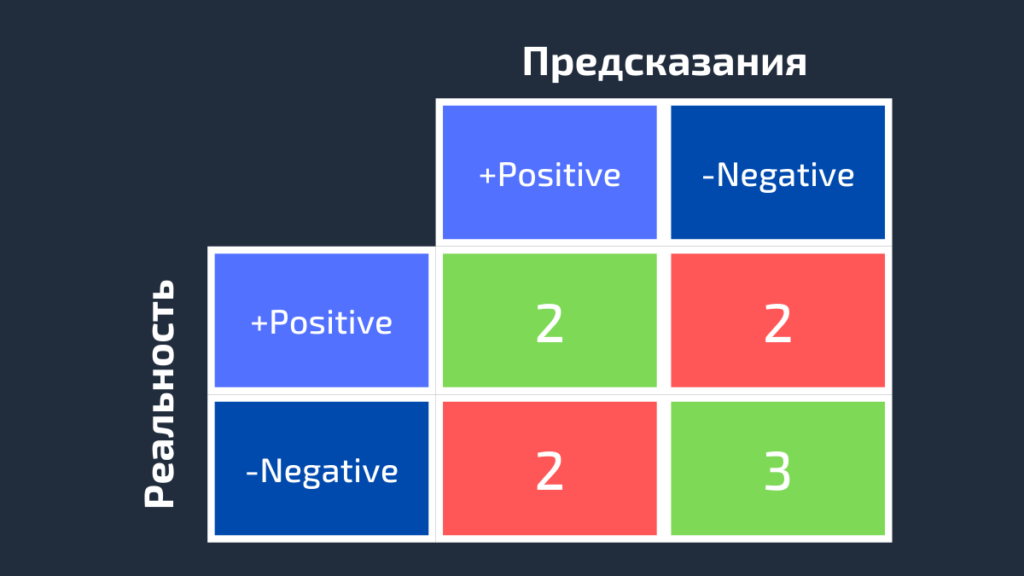
Реальность: Red, Black, Red, White, White, Red, Black, Red, White Предсказания: Red, White, Black, White, Red, Red, Black, White, RedПеред вычислением матрицы ошибок необходимо выбрать целевой класс. Давайте назначим на эту роль класс Red. Он будет отмечен как Positive, а все остальные отмечены как Negative.
Positive, Negative, Positive, Negative, Negative, Positive, Negative, Positive, Negative Positive, Negative, Negative, Negative, Positive, Positive, Negative, Negative, Positive11111111111111111111111После замены остались только два класса (Positive и Negative), что позволяет нам рассчитать матрицу ошибок, как было показано в предыдущем разделе. Стоит заметить, что полученная матрица предназначена только для класса Red.
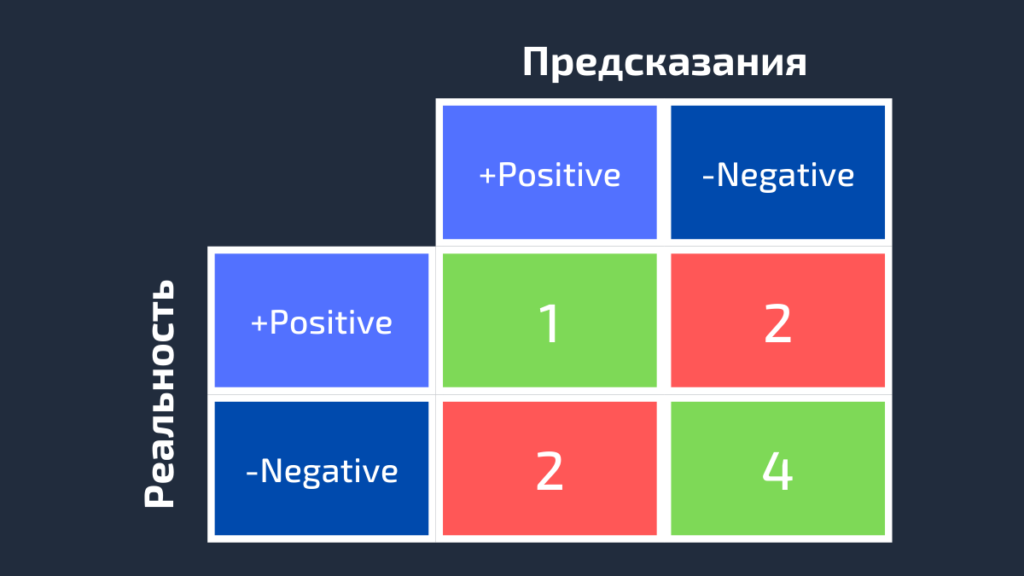
Далее для класса White заменим каждое его вхождение на Positive, а метки всех остальных классов на Negative. Мы получим такие достоверные и предсказанные метки:
Negative, Negative, Negative, Positive, Positive, Negative, Negative, Negative, Positive Negative, Positive, Negative, Positive, Negative, Negative, Negative, Positive, NegativeНа следующей схеме показана матрица ошибок для класса White.
Точно так же может быть получена матрица ошибок для Black.
Расчет матрицы ошибок с помощью Scikit-Learn
В популярной Python-библиотеке Scikit-learn есть модуль metrics, который можно использовать для вычисления метрик в матрице ошибок.
Для задач с двумя классами используется функция confusion_matrix(). Мы передадим в функцию следующие параметры:
y_true: эталонные метки.y_pred: предсказанные метки.
Следующий код вычисляет матрицу ошибок для примера двоичной классификации, который мы обсуждали ранее.
import sklearn.metrics
y_true = ["positive", "negative", "negative", "positive", "positive", "positive", "negative"]
y_pred = ["positive", "negative", "positive", "positive", "negative", "positive", "positive"]
r = sklearn.metrics.confusion_matrix(y_true, y_pred)
print(r)
array([[1, 2],
[1, 3]], dtype=int64)Обратите внимание, что порядок метрик отличается от описанного выше. Например, показатель True Positive находится в правом нижнем углу, а True Negative — в верхнем левом углу. Чтобы исправить это, мы можем перевернуть матрицу.
import numpy
r = numpy.flip(r)
print(r)
array([[3, 1],
[2, 1]], dtype=int64)Чтобы вычислить матрицу ошибок для задачи с большим числом классов, используется функция multilabel_confusion_matrix(), как показано ниже. В дополнение к параметрам y_true и y_pred третий параметр labels принимает список классовых меток.
import sklearn.metrics
import numpy
y_true = ["Red", "Black", "Red", "White", "White", "Red", "Black", "Red", "White"]
y_pred = ["Red", "White", "Black", "White", "Red", "Red", "Black", "White", "Red"]
r = sklearn.metrics.multilabel_confusion_matrix(y_true, y_pred, labels=["White", "Black", "Red"])
print(r)
array([
[[4 2]
[2 1]]
[[6 1]
[1 1]]
[[3 2]
[2 2]]], dtype=int64)Функция вычисляет матрицу ошибок для каждого класса и возвращает все матрицы. Их порядок соответствует порядку меток в параметре labels. Чтобы изменить последовательность метрик в матрицах, мы будем снова использовать функцию numpy.flip().
print(numpy.flip(r[0])) # матрица ошибок для класса White
print(numpy.flip(r[1])) # матрица ошибок для класса Black
print(numpy.flip(r[2])) # матрица ошибок для класса Red
# матрица ошибок для класса White
[[1 2]
[2 4]]
# матрица ошибок для класса Black
[[1 1]
[1 6]]
# матрица ошибок для класса Red
[[2 2]
[2 3]]В оставшейся части этого текста мы сосредоточимся только на двух классах. В следующем разделе обсуждаются три ключевых показателя, которые рассчитываются на основе матрицы ошибок.
Accuracy, Precision и Recall
Как мы уже видели, матрица ошибок предлагает четыре индивидуальных показателя. На их основе можно рассчитать другие метрики, которые предоставляют дополнительную информацию о поведении модели:
- Accuracy
- Precision
- Recall
В следующих подразделах обсуждается каждый из этих трех показателей.
Метрика Accuracy
Accuracy — это показатель, который описывает общую точность предсказания модели по всем классам. Это особенно полезно, когда каждый класс одинаково важен. Он рассчитывается как отношение количества правильных прогнозов к их общему количеству.
Рассчитаем accuracy с помощью Scikit-learn на основе ранее полученной матрицы ошибок. Переменная acc содержит результат деления суммы True Positive и True Negative метрик на сумму всех значений матрицы. Таким образом, accuracy, равная 0.5714, означает, что модель с точностью 57,14% делает верный прогноз.
import numpy
import sklearn.metrics
y_true = ["positive", "negative", "negative", "positive", "positive", "positive", "negative"]
y_pred = ["positive", "negative", "positive", "positive", "negative", "positive", "positive"]
r = sklearn.metrics.confusion_matrix(y_true, y_pred)
r = numpy.flip(r)
acc = (r[0][0] + r[-1][-1]) / numpy.sum(r)
print(acc)
# вывод будет 0.571
В модуле sklearn.metrics есть функция precision_score(), которая также может вычислять accuracy. Она принимает в качестве аргументов достоверные и предсказанные метки.
acc = sklearn.metrics.accuracy_score(y_true, y_pred)
Стоит учесть, что метрика accuracy может быть обманчивой. Один из таких случаев — это несбалансированные данные. Предположим, у нас есть всего 600 единиц данных, из которых 550 относятся к классу Positive и только 50 — к Negative. Поскольку большинство семплов принадлежит к одному классу, accuracy для этого класса будет выше, чем для другого.
Если модель сделала 530 правильных прогнозов из 550 для класса Positive, по сравнению с 5 из 50 для Negative, то общая accuracy равна (530 + 5) / 600 = 0.8917. Это означает, что точность модели составляет 89.17%. Полагаясь на это значение, вы можете подумать, что для любой выборки (независимо от ее класса) модель сделает правильный прогноз в 89.17% случаев. Это неверно, так как для класса Negative модель работает очень плохо.
Precision
Precision представляет собой отношение числа семплов, верно классифицированных как Positive, к общему числу выборок с меткой Positive (распознанных правильно и неправильно). Precision измеряет точность модели при определении класса Positive.
Когда модель делает много неверных Positive классификаций, это увеличивает знаменатель и снижает precision. С другой стороны, precision высока, когда:
- Модель делает много корректных предсказаний класса Positive (максимизирует True Positive метрику).
- Модель делает меньше неверных Positive классификаций (минимизирует False Positive).
Представьте себе человека, который пользуется всеобщим доверием; когда он что-то предсказывает, окружающие ему верят. Метрика precision похожа на такого персонажа. Если она высока, вы можете доверять решению модели по определению очередной выборки как Positive. Таким образом, precision помогает узнать, насколько точна модель, когда она говорит, что семпл имеет класс Positive.
Основываясь на предыдущем обсуждении, вот определение precision:
Precision отражает, насколько надежна модель при классификации Positive-меток.
На следующем изображении зеленая метка означает, что зеленый семпл классифицирован как Positive, а красный крест – как Negative. Модель корректно распознала две Positive выборки, но неверно классифицировала один Negative семпл как Positive. Из этого следует, что метрика True Positive равна 2, когда False Positive имеет значение 1, а precision составляет 2 / (2 + 1) = 0.667. Другими словами, процент доверия к решению модели, что выборка относится к классу Positive, составляет 66.7%.
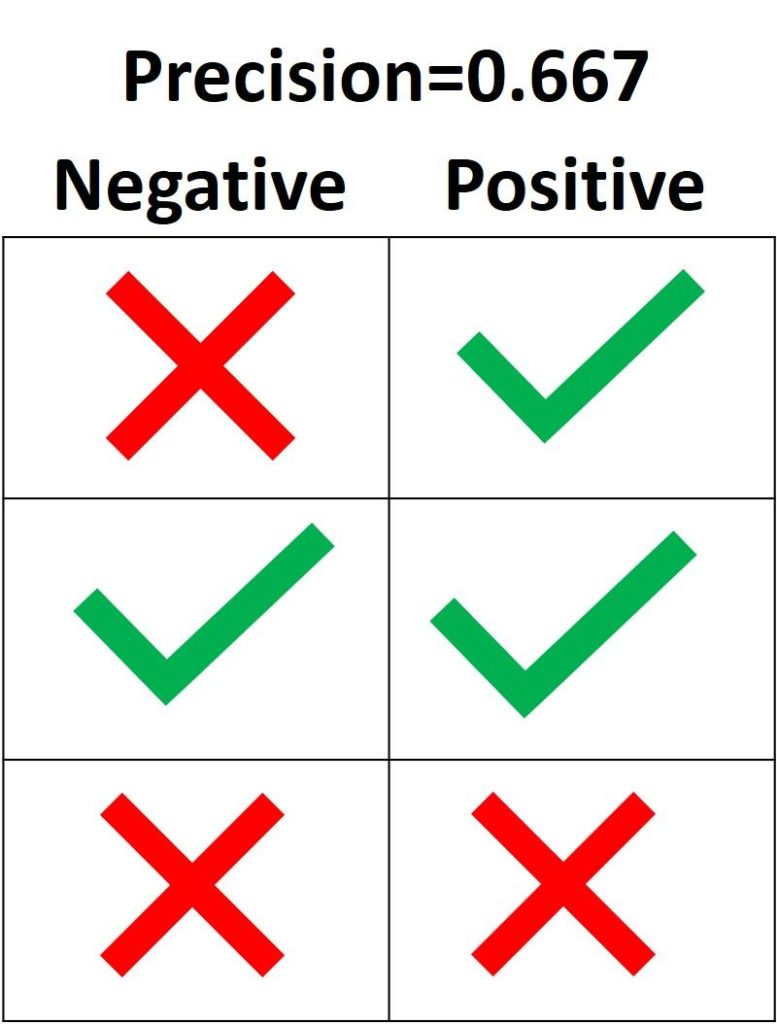
Цель precision – классифицировать все Positive семплы как Positive, не допуская ложных определений Negative как Positive. Согласно следующему рисунку, если все три Positive выборки предсказаны правильно, но один Negative семпл классифицирован неверно, precision составляет 3 / (3 + 1) = 0.75. Таким образом, утверждения модели о том, что выборка относится к классу Positive, корректны с точностью 75%.
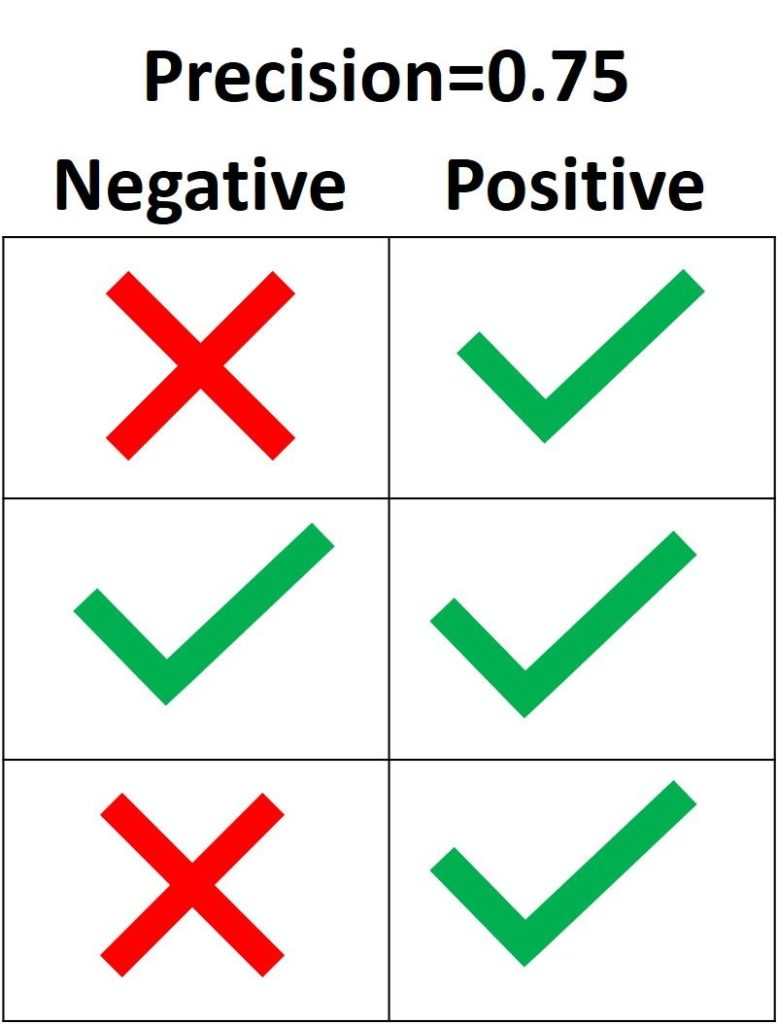
Единственный способ получить 100% precision — это классифицировать все Positive выборки как Positive без классификации Negative как Positive.
В Scikit-learn модуль sklearn.metrics имеет функцию precision_score(), которая получает в качестве аргументов эталонные и предсказанные метки и возвращает precision. Параметр pos_label принимает метку класса Positive (по умолчанию 1).
import sklearn.metrics
y_true = ["positive", "positive", "positive", "negative", "negative", "negative"]
y_pred = ["positive", "positive", "negative", "positive", "negative", "negative"]
precision = sklearn.metrics.precision_score(y_true, y_pred, pos_label="positive")
print(precision)
Вывод: 0.6666666666666666.
Recall
Recall рассчитывается как отношение числа Positive выборок, корректно классифицированных как Positive, к общему количеству Positive семплов. Recall измеряет способность модели обнаруживать выборки, относящиеся к классу Positive. Чем выше recall, тем больше Positive семплов было найдено.
Recall заботится только о том, как классифицируются Positive выборки. Эта метрика не зависит от того, как предсказываются Negative семплы, в отличие от precision. Когда модель верно классифицирует все Positive выборки, recall будет 100%, даже если все представители класса Negative были ошибочно определены как Positive. Давайте посмотрим на несколько примеров.
На следующем изображении представлены 4 разных случая (от A до D), и все они имеют одинаковый recall, равный 0.667. Представленные примеры отличаются только тем, как классифицируются Negative семплы. Например, в случае A все Negative выборки корректно определены, а в случае D – наоборот. Независимо от того, как модель предсказывает класс Negative, recall касается только семплов относящихся к Positive.

Из 4 случаев, показанных выше, только 2 Positive выборки определены верно. Таким образом, метрика True Positive равна 2. False Negative имеет значение 1, потому что только один Positive семпл классифицируется как Negative. В результате recall будет равен 2 / (2 + 1) = 2/3 = 0.667.
Поскольку не имеет значения, как предсказываются объекты класса Negative, лучше их просто игнорировать, как показано на следующей схеме. При расчете recall необходимо учитывать только Positive выборки.

Что означает, когда recall высокий или низкий? Если recall имеет большое значение, все Positive семплы классифицируются верно. Следовательно, модели можно доверять в ее способности обнаруживать представителей класса Positive.
На следующем изображении recall равен 1.0, потому что все Positive семплы были правильно классифицированы. Показатель True Positive равен 3, а False Negative – 0. Таким образом, recall вычисляется как 3 / (3 + 0) = 1. Это означает, что модель обнаружила все Positive выборки. Поскольку recall не учитывает, как предсказываются представители класса Negative, могут присутствовать множество неверно определенных Negative семплов (высокая False Positive метрика).

С другой стороны, recall равен 0.0, если не удается обнаружить ни одной Positive выборки. Это означает, что модель обнаружила 0% представителей класса Positive. Показатель True Positive равен 0, а False Negative имеет значение 3. Recall будет равен 0 / (0 + 3) = 0.
Когда recall имеет значение от 0.0 до 1.0, это число отражает процент Positive семплов, которые модель верно классифицировала. Например, если имеется 10 экземпляров Positive и recall равен 0.6, получается, что модель корректно определила 60% объектов класса Positive (т.е. 0.6 * 10 = 6).
Подобно precision_score(), функция repl_score() из модуля sklearn.metrics вычисляет recall. В следующем блоке кода показан пример ее использования.
import sklearn.metrics
y_true = ["positive", "positive", "positive", "negative", "negative", "negative"]
y_pred = ["positive", "positive", "negative", "positive", "negative", "negative"]
recall = sklearn.metrics.recall_score(y_true, y_pred, pos_label="positive")
print(recall)
Вывод: 0.6666666666666666.
После определения precision и recall давайте кратко подведем итоги:
- Precision измеряет надежность модели при классификации Positive семплов, а recall определяет, сколько Positive выборок было корректно предсказано моделью.
- Precision учитывает классификацию как Positive, так и Negative семплов. Recall же использует при расчете только представителей класса Positive. Другими словами, precision зависит как от Negative, так и от Positive-выборок, но recall — только от Positive.
- Precision принимает во внимание, когда семпл определяется как Positive, но не заботится о верной классификации всех объектов класса Positive. Recall в свою очередь учитывает корректность предсказания всех Positive выборок, но не заботится об ошибочной классификации представителей Negative как Positive.
- Когда модель имеет высокий уровень recall метрики, но низкую precision, такая модель правильно определяет большинство Positive семплов, но имеет много ложных срабатываний (классификаций Negative выборок как Positive). Если модель имеет большую precision, но низкий recall, то она делает высокоточные предсказания, определяя класс Positive, но производит всего несколько таких прогнозов.
Некоторые вопросы для проверки понимания:
- Если recall равен 1.0, а в датасете имеются 5 объектов класса Positive, сколько Positive семплов было правильно классифицировано моделью?
- Учитывая, что recall составляет 0.3, когда в наборе данных 30 Positive семплов, сколько представителей класса Positive будет предсказано верно?
- Если recall равен 0.0 и в датасете14 Positive-семплов, сколько корректных предсказаний класса Positive было сделано моделью?
Precision или Recall?
Решение о том, следует ли использовать precision или recall, зависит от типа вашей проблемы. Если цель состоит в том, чтобы обнаружить все positive выборки (не заботясь о том, будут ли negative семплы классифицированы как positive), используйте recall. Используйте precision, если ваша задача связана с комплексным предсказанием класса Positive, то есть учитывая Negative семплы, которые были ошибочно классифицированы как Positive.
Представьте, что вам дали изображение и попросили определить все автомобили внутри него. Какой показатель вы используете? Поскольку цель состоит в том, чтобы обнаружить все автомобили, используйте recall. Такой подход может ошибочно классифицировать некоторые объекты как целевые, но в конечном итоге сработает для предсказания всех автомобилей.
Теперь предположим, что вам дали снимок с результатами маммографии, и вас попросили определить наличие рака. Какой показатель вы используете? Поскольку он обязан быть чувствителен к неверной идентификации изображения как злокачественного, мы должны быть уверены, когда классифицируем снимок как Positive (то есть с раком). Таким образом, предпочтительным показателем в данном случае является precision.
Вывод
В этом руководстве обсуждалась матрица ошибок, вычисление ее 4 метрик (true/false positive/negative) для задач бинарной и мультиклассовой классификации. Используя модуль metrics библиотеки Scikit-learn, мы увидели, как получить матрицу ошибок в Python.
Основываясь на этих 4 показателях, мы перешли к обсуждению accuracy, precision и recall метрик. Каждая из них была определена и использована в нескольких примерах. Модуль sklearn.metrics применяется для расчета каждого вышеперечисленного показателя.




![[Опрос] Насколько популярен Python в 2021, главный приз — MacBook Pro Насколько популярен Python в 2021](https://pythonru.com/wp-content/uploads/2021/06/naskolko-populyaren-python-v-2021-218x150.png)


