Я думаю, что большинство людей слышали о ROC-кривой или о AUC (площади под кривой) раньше. Особенно те, кто интересуется наукой о данных. Однако, что такое ROC-кривая и почему площадь под этой кривой является хорошей метрикой для оценки модели классификации?
Теория ROC-кривой
Полное название ROC — Receiver Operating Characteristic (рабочая характеристика приёмника). Впервые она была создана для использования радиолокационного обнаружения сигналов во время Второй мировой войны. США использовали ROC для повышения точности обнаружения японских самолетов с помощью радара. Поэтому ее называют рабочей характеристикой приемника.
AUC или area under curve — это просто площадь под кривой ROC. Прежде чем мы перейдем к тому, что такое ROC-кривая, нужно вспомнить, что такое матрица ошибок.
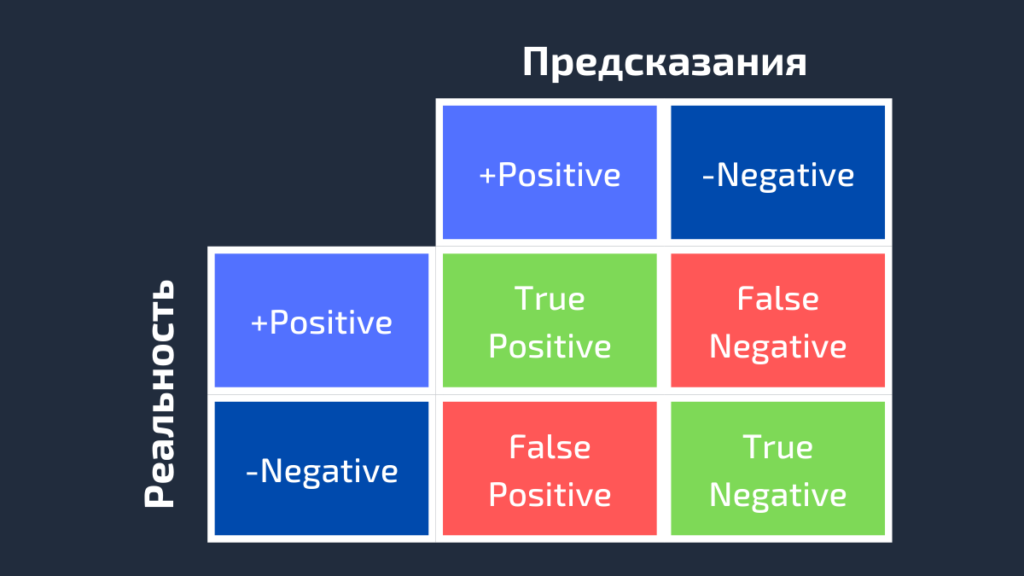
Как видно из рисунка выше, матрица ошибок — это комбинация вашего прогноза (1 или 0) и фактического значения (1 или 0). В зависимости от результата предсказания и того, корректна ли была проведена классификация, матрица разделена на 4 части. Например, true positive (истинно положительный) результат — это количество случаев, в которых вы правильно классифицируете семпл как положительный. А false positive (ложноположительный) — это число случаев, в которых вы ошибочно классифицируете семпл как положительный.
Матрица ошибок содержит только абсолютные числа. Однако, используя их, мы можем получить множество других метрик, основанных на процентных соотношениях. True Positive Rate (TPR) и False Positive Rate (FPR) — две из них.
True Positive Rate (TPR) показывает, какой процент среди всех positive верно предсказан моделью.
TPR = TP / (TP + FN).
False Positive Rate (FPR): какой процент среди всех negative неверно предсказан моделью.
FPR = FP / (FP + TN).
Хорошо, давайте теперь перейдем к кривой ROC!
Что такое ROC-кривая?
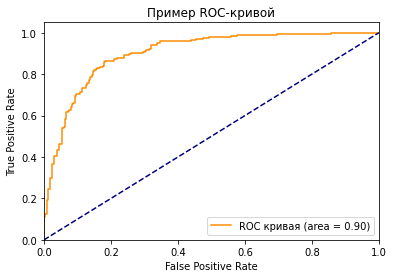
Как вы можете видеть на графике, кривая ROC — это просто отношение TPR к FPR. Теперь вам все понятно, в заключение…
Поверили?
Если серьезно, вы можете прочитать намного больше информации из диаграммы. Первый вопрос, который я хочу здесь обсудить: у нас же есть только один набор TPR, FPR, посчитанный на основе сделанных моделью предсказаний. Так откуда взялось такое количество точек для построения целого графика?
Все следует из того, как работает модель классификации. Когда вы строите классификационную модель, такую как дерево решений, и хотите определить, будут ли акции расти в цене или падать на основе входных данных. Модель сначала рассчитает вероятность увеличения или уменьшения, используя предоставленные вами исторические данные. После этого, основываясь на пороговом значении, она решит, будет ли результат увеличиваться или уменьшаться.
Да, ключевое слово здесь — порог. Разные пороговые значения создают разные TPR и FPR. Они представляют те самые точки, что образуют кривую ROC. Вы можете выбрать «Увеличение» в качестве предсказания модели, если полученная на основе исторических данных вероятность роста акций больше 50%. Также можете изменить пороговое значение и отобразить «Увеличение», только если соответствующая вероятность больше 90%. Если вы установите 90% порог вместо 50%, вы будете более уверены в том, что выбранные для «Увеличения» акции действительно вырастут. Но так вы можете упустить некоторые потенциально выгодные варианты.
Что значит синяя пунктирная линия на графике?
Как мы знаем, чем больше площадь под кривой (AUC), тем лучше классификация. Идеальная или наилучшая кривая — это вертикальная линия от (0,0) до (0,1), которая тянется до (1,1). Это означает: модель всегда может различить положительные и отрицательные случаи. Однако, если вы выбираете класс случайным образом для каждого семпла, TPR и FPR должны увеличиваться с одинаковой скоростью. Синяя пунктирная линия показывает кривую TPR и FPR при случайном определении positive или negative для каждого случая. Для этой диагональной линии площадь под кривой (AUC) составляет 0.5.
Что произойдет с TPR, FPR и ROC-кривой, если изменить пороговое значение?
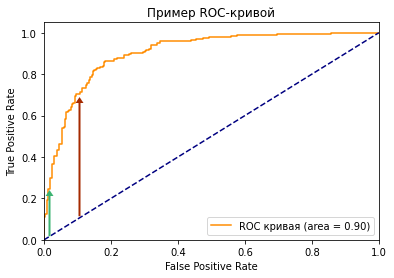
Посмотрите на две точки на ROC-кривой. Зеленая точка имеет очень высокий порог, это означает, что только если вы уверены на 99%, можете классифицировать случай как positive. Красная точка имеет относительно более низкий порог. Это означает, что вы можете классифицировать случай как positive, если вы уверены на 90%.
Как изменяются TPR и FPR при движении от зеленой точки к красной?
И TPR, и FPR увеличиваются. Когда вы уменьшаете порог, модель будет определять больше положительных случаев. Таким образом, TP увеличивается, как и TP/(TP + FN). С другой стороны, вы неизбежно ошибочно классифицируете некоторые отрицательные случаи как положительные из-за снижения порога, и поэтому FP и FP/(FP + TN) также увеличиваются.
Мы видим, что TPR и FPR положительно коррелируют. Вам нужно балансировать между максимальным охватом positive случаев и минимизацией неправильной классификации negative случаев.
Как выбрать оптимальную точку на кривой ROC?
Трудно определить оптимальную точку, потому что нужно выбрать наиболее подходящее пороговое значение, учитывая сферу применения модели. Однако общее правило — максимизировать разницу (TPR-FPR), которая на графике представлена вертикальным расстоянием между оранжевой и синей пунктирной линией.
Почему площадь под кривой ROC – хорошая метрика для оценки модели классификации?
Хорошая метрика модели машинного обучения должна отображать истинную и постоянную способность модели к прогнозированию. Это означает, что, если я изменю тестовый набор данных, он не должен давать другой результат.
ROC-кривая учитывает не только результаты классификации, но и вероятность предсказания всех классов. Например, если результат корректно классифицирован на основе 51% вероятности, то он, скорее всего, будет классифицирован неверно, если вы воспользуетесь другим тестовым датасетом. Кроме того, ROC-кривая также учитывает эффективность модели при различных пороговых значениях. Она является комплексной метрикой для оценки того, насколько хорошо разделяются случаи в разных группах.
Какое значение AUC является приемлемым для модели классификации?
Как я показал ранее, для задачи двоичной классификации при определении классов случайным образом, вы можете получить 0.5 AUC. Следовательно, если вы решаете задачу бинарной классификации, разумное значение AUC должно быть > 0.5. У хорошей модели классификации показатель AUC > 0.9, но это значение сильно зависит от сферы ее применения.
Как рассчитать AUC и построить ROC-кривую в Python?
Если вы просто хотите рассчитать AUC, вы можете воспользоваться пакетом metrics библиотеки sklearn (ссылка).
Если вы хотите построить ROC-кривую для результатов вашей модели, вам стоит перейти сюда.
Вот код для построения графика ROC, который я использовал в этой статье.
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_curve, auc
from sklearn.metrics import roc_auc_score
from matplotlib import pyplot as plt
# генерируем датасет на 2 класса
X, y = make_classification(n_samples=1000, n_classes=2, random_state=1)
# разделяем его на 2 выборки
trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2)
# обучаем модель
model = LogisticRegression(solver='lbfgs')
model.fit(trainX, trainy)
# получаем предказания
lr_probs = model.predict_proba(testX)
# сохраняем вероятности только для положительного исхода
lr_probs = lr_probs[:, 1]
# рассчитываем ROC AUC
lr_auc = roc_auc_score(testy, lr_probs)
print('LogisticRegression: ROC AUC=%.3f' % (lr_auc))
# рассчитываем roc-кривую
fpr, tpr, treshold = roc_curve(testy, lr_probs)
roc_auc = auc(fpr, tpr)
# строим график
plt.plot(fpr, tpr, color='darkorange',
label='ROC кривая (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Пример ROC-кривой')
plt.legend(loc="lower right")
plt.show()
Вам нужны следующие входные данные: фактическое значение y и вероятность предсказания. Обратите внимание, что функция roc_curve требует только вероятность для положительного случая, а не для обоих классов. Если вам нужно решить задачу мультиклассовой классификации, вы также можете использовать этот пакет, и в приведенной выше ссылке есть пример того, как построить график.
