Пишем нейронную сеть для игры в блэкджек на python ~ PythonRu

В предыдущем материале был написан код для симуляции игры в блэкджек. С помощью симуляции большого количества игр можно было четко отследить, какое преимущество есть у казино. Вот что удалось обнаружить:

Казино получает конкурентное преимущество, заставляя игроков совершать действия до дилера (действовать в условиях неполной информации). Это создает риск получить перебор (таким образом игроки теряют все еще до того, как дилер совершает хоть какое-нибудь действие).
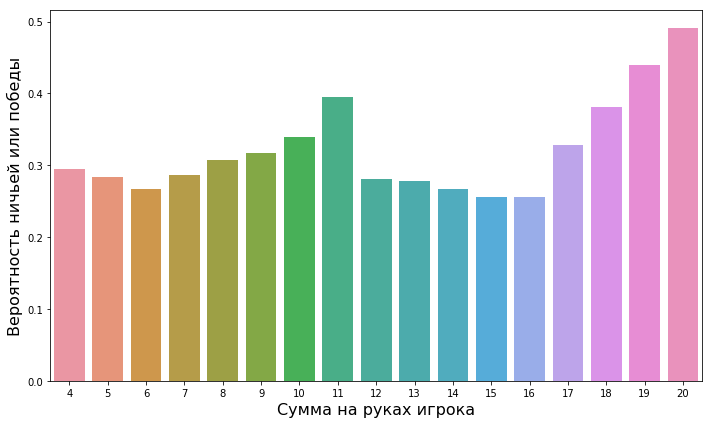
Особую опасность представляют ситуации, когда карты на руках игроков стоят от 12 до 16 очков (в таком случае вероятность получить перебор со следующей картой максимальная), а дилер показывает старшую карту. В таких случаях можно предположить, что у дилера будет более высокое значение, так что игрокам остается только брать еще или проигрывать. Это можно увидеть даже визуально на графике с шансами на победу или ничью (промежуток значений от 12 до 16 называется “долиной отчаяния”).
Наконец, простейшая «наивная» стратегия брать карты в случае нулевой вероятности получить перебор значительно увеличивает шансы на победу, ведь в таком случае растет вероятность того, что проиграет казино.

Также в том материале были описаны и правила игры.

Способно ли глубокое обучение справиться лучше?

Задача этого материала — определить, можно ли с помощью глубокого обучения получить более эффективную стратегию. Для этого:

Сгенерируем данные с помощью симулятора блэкджека из прошлого материала (с некоторыми исправлениями, чтобы он лучше подходил для тренировки алгоритмов).
Напишем код для тренировки нейронной сети игре в блэкджек (желательно оптимальной).

Прежде чем переходить к самому процессу тренировки, вернемся и быстро рассмотрим достоинства и недостатки использования нейронной сети в этой ситуации. Нейронные сети — это очень эффективные алгоритмы, которые можно, грубо говоря, сравнить с глиной. Они подстраиваются под очертания доступной информации, при это минимально или вообще не изменяясь. Данные, например, с линейной регрессией запросто поддаются обработке с помощью нейронной сети. А слои и нейроны в сети способны находить заложенные глубоко внутри нелинейные отношения данных.

Тем не менее за такую гибкость приходится платить: нейронная сеть — это модель черного ящика. В отличие от регрессии, когда можно увидеть, как именно модель принимает решения, посмотрев на коэффициенты, нейронная сеть такой прозрачностью не обладает. Она также подвержена риску переобучения, при котором данные из выборки уже не обобщаются. Об этих недостатках нужно помнить и предпринимать дополнительные меры для работы с ними. Тем не менее это не повод отказываться от использования нейронных сетей.

Генерация тренировочных данных

Перед началом тренировки нейронной сети сперва нужно определить, как структурировать данные так, чтобы построенная модель была полезной.

Что нужно предсказать? Есть два кандидата на роль целевой переменной:

Вероятность поражения. Но это полезно только в том случае, если бы была возможность увеличить или уменьшить ставку, однако в блэкджеке такого варианта нет.
Оптимальное действие: взять еще карту или спасовать. Поэтому целевой переменной будет решение о том, какое действие идеально в конкретной ситуации: взять еще или сделать пас.

Нет необходимости в том, чтобы сеть вообще не делала ошибок. Достаточно добиться того, чтобы она в большинстве случаев предсказывала правильно. Вот какой способ для этого можно использовать:

раздать карты игроку и дилеру;
проверить, нет ли у одного из них 21;
выполнить одно действие (взять карту или спасовать);
симулировать игру до конца и записать результат.

Поскольку симулируемый игрок принимает лишь одно решение, можно оценить его качество на основе того, выиграл ли он партию или проиграл:

Если игрок взял карту и выиграл, тогда карта (Y=1) была правильным решением
Если игрок взял карту и проиграл, тогда пас (Y=0) был правильным решением
Если игрок спасовал и выиграл, тогда пас (Y=1) был правильным решением
Если игрок спасовал и проиграл, тогда карта (Y=0) была правильным решением

Это позволяет тренировать модель так, чтобы вывод представлял собой предсказание правильного действия: карта или пас. Код похож на тот, что использовался в прошлый раз. Вот основные признаки:

Открытая карта лидера (вторая закрыта от игроков)
Общая стоимость карт в руках игрока
Проверка, есть ли у игрока туз
Действие игрока (карта или пас)

Цель — выявить правильно решение на основе описанный выше логики.

Тренировка нейронной сети

ВАЖНО! Весь код статьи в этом архиве

Для нейронной сети будет использоваться библиотека Keras. Сначала добавим все необходимые импорты:

from keras.models import Sequential
from keras.layers import Dense, LSTM, Flatten, Dropout

Теперь настроим переменные ввода для тренировки сети. feature_list — это переменная с колонками, представляющими перечисленные выше признаки. В dataframe model_rf хранятся данные запущенных симуляций.

# Задаем переменные для нейронной сети
feature_list = [i for i in model_df.columns if i not in  
['dealer_card','Y','lose','correct_action']  
]  
train_X = np.array(model_df[feature_list])  
train_Y = np.array(model_df['correct_action']).reshape(-1,1)

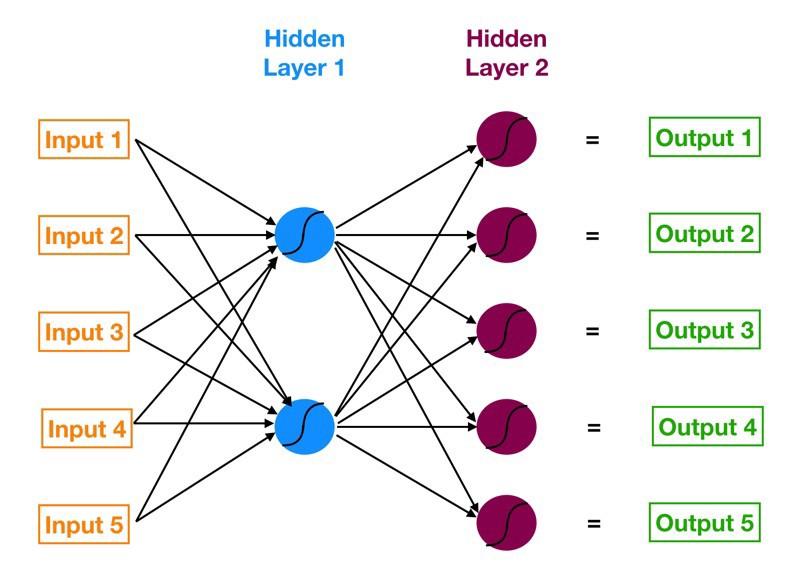
Код, запускающий и тренирующий нейронную сеть, довольно простой. Первая строка создает нейронную сеть последовательного типа, которая является линейной последовательностью слоев нейронной сети. Следующие строки друг за другом добавляют слои (Dense — простейший тип слоя, представляющий собой набор нейронов), а числа 16, 128 и т. д. обозначают количество нейронов в каждом слое.

Наконец, для последнего слоя нужно выбрать функцию активации. Она конвертирует сырой вывод в более осмысленный вид. Обратите внимание на две вещи: во-первых, финальный слой включает лишь один нейрон, потому что предсказание делается на основе двух возможных выводов (двухклассовая проблема). Во-вторых, используется сигмоидная функция, потому что необходимо, чтобы нейронная сеть действовала по принципу логистической регрессии и предсказывала, что является корректным действием: карта (Y=1) или пас (Y=0). Другими словами, необходимо знать вероятность того, что карта — это правильный вариант.

Последние две строчки сообщают, какую функцию потерь использовать (перекрестная функция — это функция потерь, используемая классификационными моделями, которые предсказывают вероятности) и сопоставляют данные с моделью. Если поэкспериментировать с количеством нейронов чуть дольше, то можно получить еще более эффективную сеть.

# Настройка нейронной сети с 5 слоями
model = Sequential()
model.add(Dense(16))
model.add(Dense(128))
model.add(Dense(32))
model.add(Dense(8))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='sgd')
model.fit(train_X, train_Y, epochs=20, batch_size=256, verbose=1)

pred_Y_train = model.predict(train_X)
actuals = train_Y[:,-1]

Предсказание производительности модели

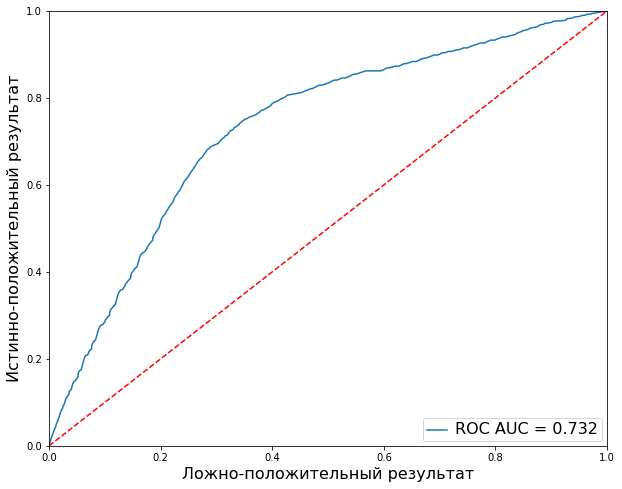
Простой способ оценить, насколько эффективнее оказывается модель — использовать ROC-кривую. ROC-кривая показывает, насколько хороша модель в плане отношения между пользой (общим количеством носителей признака, верно классифицированных как несущие признак) и затратами (долей объектов от общего количества объектов, не несущих признака, ошибочно классифицированных как несущие признак). Чем больше площадь под кривой, тем лучше модель.

График показывает ROC-кривую для нейронной сети, играющей в блэкджек. Судя по всему, она все-таки дает обеспечивает полезность относительно случайного угадывания (красная пунктирная линия). Площадь под кривой, AUC, — 0,73, в то время как показатель AUC для случайного предсказывания равен 0,5.

Для составления ROC-кривой здесь использовались тренировочные данные. Обычно для этого нужны тестовые данные, но в этом случае, поскольку известно, что набор довольно большой, то он является репрезентативным (если продолжать играть по тем же правилам). И можно предположить, что модель будет хорошо обобщать данные (любые новые данные будут обладать теми же характеристиками, что и тренировочные).

Время играть!

Прежде чем нейронная сеть начнет играть, ей нужно передать правило принятия решения. Здесь нужно напомнить, что сигмоидная активация (из финального слоя нейронной сети) показывает вывод в виде вероятности того, что карта — это правильный ход. Теперь нужно задать правила, когда в соответствии с вероятностью необходимо брать карту или делать пас.

Функция mode_decision принимает в качестве признаков то, что необходимо нейронной сети, делает на их основе предсказание и сравнивает его с заданным порогом, чтобы решить, брать или еще карту или пасовать. Используем значение 0,52, потому что нам известно, что перебор в блэкджеке представляет куда большую опасность. Таким образом такая вероятность слегка уменьшает вероятность действия карта и уменьшает риск перебора.

# Учитывая входные данные, функция использует нейронную сеть, чтобы сделать прогноз
# а затем на основе этого прогноза решает, взять или пропустить

def model_decision(model, player_sum, has_ace, dealer_card_num):
    input_array = np.array([player_sum, 0, has_ace, dealer_card_num]).reshape(1,-1)
    predict_correct = model.predict(input_array)
    if predict_correct >= 0.52:
        return 1
    else:
        return 0

Осталось лишь добавить эту функцию в код в то место, где решается, брать ли еще карту или пасовать. Теперь нейронная сеть будет принимать решение на основе того, какую карту показывает дилер, общей стоимости карт и наличия туза в руке.

А модель хороша!

Теперь сравним показатели нейронной сети со случайной и наивной стратегиями.

Всего было запущено 300 000 симуляций для каждой стратегии
При наивной стратегии карта берется только в том случае, если на руках меньше 12 очков
При случайной стратегии подбрасывается монетка: если орел, тогда берем карту, если решка — пас. Если карта взята и нет перебора, тогда процесс продолжается снова и снова.

Посмотрим, получилась ли стратегия нейронной сети более выгодной. Следующая таблица показывает распределение результата для каждой стратегии. Нейронная сеть проиграла чуть меньше половины сыгранных игр. В этом случае вы все еще не обыгрываете казино, но это неплохой результат для игры, где все шансы против игрока. При этом ей не удалось одержать намного больше побед, чем в случае наивной стратегии — зато получилось больше ничьих.

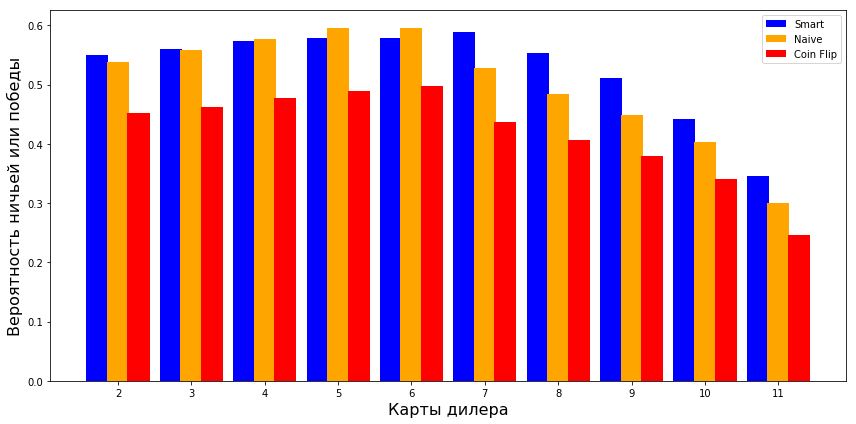
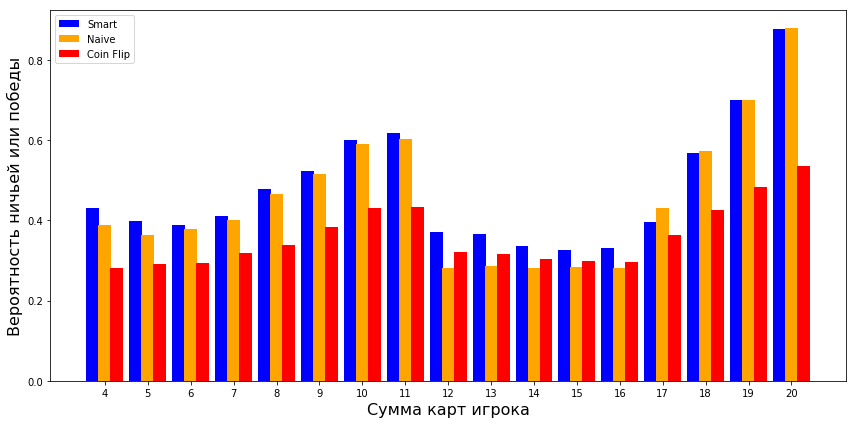
Также можно взглянуть на то, как показали себя стратегии в отношении ключевых признаков (карты дилера и стоимости карт на руках). Во-первых, проверим, как карта дилера влияет на вероятность победы или ничьей в трех стратегиях. Если у дилера карта с маленьким значением, результаты нейронной сети такие же, как и у наивной стратегии. Но если у него больше 7, то она показывает себя намного лучше.

Также можно взглянуть на вероятность победы или ничьей в зависимости от стартовой руки игрока. Нам всем диапазоне нейронная сеть показывает себя намного эффективнее. И в отличие от наивной, которая работает даже хуже угадывания в долине отчаяния (когда на руках значения от 12 до 16), нейронная сеть выступает очень неплохо.

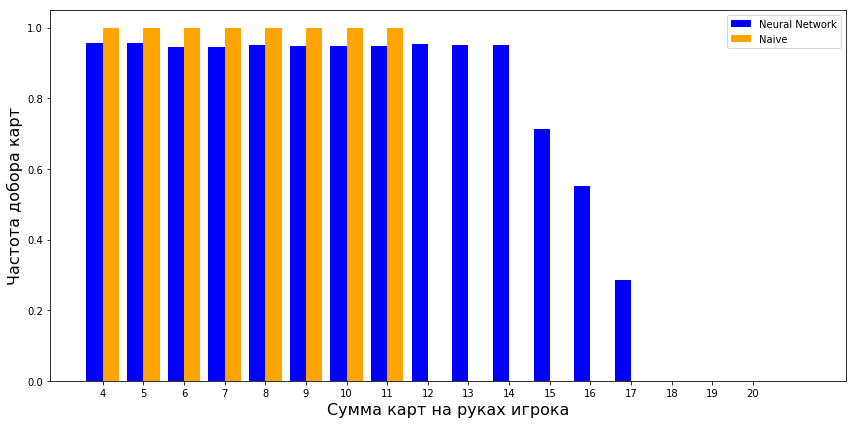
Следующий график показывает, насколько нейронная сеть эффективнее наивной стратегии. Последняя (из-за используемого алгоритма) даже не предпринимает попыток, когда есть хоть какая-то вероятность перебора. Нейронная сеть же регулярно берет еще карту, когда у нее 12, 13, 14 или 15. В данном случае речь идет о принятии решений с большим количество деталей и способностью учитывать некоторые риски.

Можно взглянуть на то, что делает нейронная сеть, когда у игрока на руках между 12 и 16 очками, чтобы улучшить наивную стратегию (и не проигрывать так много денег казино).

Похоже, что сеть часто берет карту, когда дилер показывает старшую карту (8, 9 или 10). Но даже когда у него на руках что-то низкое, например 3, нейронная сеть берет карту в 60% случаев. Это связано с тем, что она учитывает все признаки. На основе этого можно было бы разработать несколько простых правил.

Выводы

Теперь вы должны чуть лучше представлять, как машинное обучение используется для помощи в принятии решений из реальной жизни. Вот что важно запомнить для тренировки моделей (будь то деревья решений, регрессии или нейронные сети):

Структурирована ли целевая переменная так, что если ее можно предсказать, то она решит проблему? Прежде чем переходить к сбору данных и построению модели, важно убедиться, что вы предсказываете нужные вещи.
Как могут новые данные отличаться от тех, на которых производилась тренировка? Если они будут отличаться значительно, тогда статистическая модель может и вовсе не подойти. И по крайней мере это нужно осознавать и встраивать проверки, такие как регуляризация или строгая валидация, а также проводить тестирование модели.
Если вы не можете понять, как модель принимает решения, то не поймете качество этих решений, сделанных вне тестовых данных.

Напоследок пара напутственных слов о том, как вы сможете улучшить представленный код самостоятельно:

Попробуйте улучшить модель с помощью оптимизированной структуры нейронной сети, кода для разделения тузов (здесь он не использовался) или, наконец, выбора лучших признаков.
Научите модель считать карты и смотрите, как это влияет на производительность в случае игры с одной колодой и шестью (стандарт Вегаса).

Возможно, вам удастся добиться более впечатляющих результатов. Удачи!