Играем в блэкджек на Python

Познакомьтесь с реализацией популярной карточной игры блэкджек, которая предоставит возможность осознать все риски поездки в Лас-Вегас.

Это руководство не ставит за цель рекламу блэкджека или любых других азартных игр. В казино все ставки всегда против вас, так что со временем вы ВСЕГДА теряете деньги. Никогда не рискуйте тем, что не готовы потерять.

Один из классических видов приложений на тему вероятности и статистики — это изучение азартных игр. Они так любимы среди специалистов по статистике, потому что содержат элементы как случайности, так и определенной неизбежности:

• Случайность в том, что вы никогда не знаете, чего ждать от игры.
• Неизбежность — знание среднего результата для большого количества сыгранных партий.

В этом материале будем разбираться с блэкджеком, написав симулятор на Python. Потом проведем несколько симуляций и изучим, как себя вел игрок. Если вдруг не помните правила этой игры, то вот ключевые моменты:

1. Игроки делают ставки
2. Им выдают по 2 карты в закрытом виде
3. Дилер также получает 2 карты, но одна из них видна игрокам.
4. Цель игры — набрать больше очков, чем у дилера (но не больше 21, больше 21 — это автоматическое поражение, которое называется перебор). Если удалось набрать больше очков, чем у дилера, то выигрышем является ставка (победа также присуждается, если у дилера перебор). Тузы оцениваются в 1 или 11 очков, а все остальные карты — согласно их значениям (валет, дама и король — их называют “картинками” — в 10 очков).
5. Лучшая стартовая комбинация — туз и картинка. Она называется блэкджек.
6. После первого раунда у каждого игрока есть возможность взять больше карт или спасовать (не брать карт). Если игрок набрал больше 21 очка, то его ставка сгорает.
7. Когда все игроки решили, что не будут больше брать карты, дилер переворачивает свою скрытую карту. Если у него меньше 17 очков, то он обязан взять еще. Так продолжается до тех пор, пока он не наберет 17 или больше.
8. После этого подводятся итоги. Если у дилера перебор, тогда игроки без перебора получают свои ставки. Если нет — тогда набранные значения сравниваются. Каждый, кто набрал больше дилера, выигрывает сумму равную ставке. Тот, у кого меньше, теряет поставленное. В случае ничьей деньги остаются на местах.

А теперь пришло время программирования

Для удобства и избежания ошибок используйте этот black_jack.ipynb

Создание симулятора

Неплохо было бы использовать ООП, но не в этот раз. Вы сами можете попробовать сделать рефакторинг и реализовать финальный код по правилам в ООП.

Для начала добавим необходимые импорты:

import numpy as np  
import pandas as pd  
import random  
import matplotlib.pyplot as plt  
import seaborn as sns

Теперь создадим кое-какие функции. Во-первых, нужна та, что будет создавать новую колоду карт. За эту операцию будет отвечать make_decks. Она должна добавлять 4 масти каждой карты (туза, двойки, тройки, четверки и так далее) в список new_deck, перемешивать его и возвращать новый список, с которым предстоит играть. В функции можно указать и количество колод (num_decks), которые должна создавать функция.

# Создаем колоду
def make_decks(num_decks, card_types):
    new_deck = []
    for i in range(num_decks):
        for j in range(4):
            new_deck.extend(card_types)
    random.shuffle(new_deck)
    return new_deck

Также нужна функция, которая будет прибавлять значения карт в руке. Это сложнее базовой операции прибавления, потому что, например, туз может быть равен 1 или 11 в зависимости от того, что выгодно владельцу. Поэтому в первую очередь функция подсчитывает значение всех карт в руке за исключением туза (все картинки могут быть представлены в виде 10, поскольку в блэкджеке они работают идентично). Затем она подсчитывает количество тузов. Наконец, определяет, сколько должен «стоить» туз в зависимости от значений остальных карт в руке.

Вспомогательная функция ace_values принимает в качестве аргумента количество тузов в руке и выдает список уникальных значений стоимости тузов:

# Эта функция перечисляет все комбинации значений туза в  
# массив sum_array.  
# Например, если у вас 2 туза, есть 4 комбинации:  
# [[1,1], [1,11], [11,1], [11,11]]  
# Эти комбинации приводят к 3 уникальным суммам: [2, 12, 22]  
# Из этих 3 только 2 являются <= 21, поэтому они возвращаются: [2, 12]+
def get_ace_values(temp_list):  
    sum_array = np.zeros((2**len(temp_list), len(temp_list)))  
    # Этот цикл получает комбинации
    for i in range(len(temp_list)):  
        n = len(temp_list) - i  
        half_len = int(2**n * 0.5)  
        for rep in range(int(sum_array.shape[0]/half_len/2)):  
            sum_array[rep*2**n : rep*2**n+half_len, i]=1  
            sum_array[rep*2**n+half_len : rep*2**n+half_len*2, i]=11  
    # Только значения, которые подходят (<=21)  
    return list(set([int(s) for s in np.sum(sum_array, axis=1)\  
                     if s<=21]))  # Конвертация num_aces, int в list
                       
# Например, если num_aces = 2, вывод должен быть [[1,11],[1,11]]  
# Нужен этот формат для функции get_ace_values
def ace_values(num_aces):  
    temp_list = []  
    for i in range(num_aces):  
        temp_list.append([1,11])  
    return get_ace_values(temp_list)

Эти две функции могут быть использованы функцией total_up, которая рассчитывает стоимость всех карт в руке (включая правильную обработку любого количества тузов):

# Сумма на руках
def total_up(hand):
    aces = 0
    total = 0
    
    for card in hand:
        if card != 'A':
            total += card
        else:
            aces += 1
    
    # Вызовите функцию ace_values, чтобы получить список возможных значений для тузов на руках.
    ace_value_list = ace_values(aces)
    final_totals = [i+total for i in ace_value_list if i+total<=21]
    
    if final_totals == []:
        return min(ace_value_list) + total
    else:
        return max(final_totals)

Когда со вспомогательными функциями покончено, можно переходить к основному циклу. Сначала определяют ключевые переменные:

• stacks — количество стеков карт (где каждый стек может состоять из одной или большего количества колод), которые будут симулироваться
• players — количество игроков в одной партии
• num_decks — количество колод в каждом стеке
• card_types — список всех 13 типов карт

stacks = 50000
players = 1
num_decks = 1

card_types = ['A',2,3,4,5,6,7,8,9,10,10,10,10]

Дальше начинаются основные циклы симулятора. Всего их два:

1. Цикл for перебирает 50 000 симулируемых стеков карт
2. Цикл while, по одному для каждого стека, играет в блэкджек до тех пор, пока в стеке не осталось 20 или меньше карт. В этот момент он переходит к следующему стеку

Массив numpy, curr_player_results, — это важная переменная, где хранятся результаты каждого игрока: 1 — победа, 0 — ничья, -1 — поражение. Каждый элемент массива соответствует одному игроку за столом.

В цикле while каждый игрок и дилер получают по карте (фрагмент с комментарием # Получение ПЕРВОЙ карты). После этого все получают еще по одной карте. Для этого используется функция pop с аргументом 0 — она возвращает первый элемент списка, удаляя его из списка (идеально подходит для работы с картами в стеке). Когда в стеке дилера меньше 20 карт, новый стек заменяет предыдущий (переходит к следующей итерации цикла for).

for stack in range(stacks):
    blackjack = set(['A',10])
    dealer_cards = make_decks(num_decks, card_types)
    while len(dealer_cards) > 20:
        
        curr_player_results = np.zeros((1,players))
        
        dealer_hand = []
        player_hands = [[] for player in range(players)]

        # Получение ПЕРВОЙ карты
        for player, hand in enumerate(player_hands):
            player_hands[player].append(dealer_cards.pop(0))
        dealer_hand.append(dealer_cards.pop(0))
        # Получение ВТОРОЙ карты
        for player, hand in enumerate(player_hands):
            player_hands[player].append(dealer_cards.pop(0))
        dealer_hand.append(dealer_cards.pop(0))

Дальше дилер проверяет, нет ли у него блэкджека (туз и 10). Обратите внимание, что блэкджек определен как множество, включающее туз (ace) и десятку.

Если у дилера блэкджек, тогда игроки проиграли (они получают соответствующее значение -1 в curr_player_results). Это касается только тех, у кого также не выпало 21 очков (в этом случае объявляется ничья).

# Дилер проверяется на 21
        if set(dealer_hand) == blackjack:
            for player in range(players):
                if set(player_hands[player]) != blackjack:
                    curr_player_results[0,player] = -1
                else:
                    curr_player_results[0,player] = 0

Если дилер не получил блэкджек, тогда игра продолжается. Теперь игроки проверяют, нет ли у них победной комбинации. Если есть — они автоматически одерживают победу (в некоторых казино это подразумевает выплату 1,5 к 1, то есть вы можно получить $150 в ответ на ставку $100). Выигрыш записывается с помощью значения 1 в массиве curr_player_results соответствующего игрока.

Игроки без блэкджека получают возможность взять новые карты или спасовать. В этой симуляции цель была в том, чтобы захватить все виды решений игрока — умные, глупые и удачные. Поэтому решение основывается на броске монетки (если random.random() генерирует значение больше 0,5, тогда игрок берет еще карту, в противном случае — пасует).

Такой подход может показаться глупым, но именно за счет того, что решение не связано с происходящим в игре, можно изучить все ситуации и сгенерировать богатый набор данных для анализа.

Прямо сейчас нет необходимости определять оптимальную стратегию. Задача симулятора — сгенерировать тренировочные данные, с помощью которых можно тренировать нейронную сеть играть в блэкджек оптимально.

В Python символ \ обозначает продолжение строки. Он используется для создания длинных строк кода и улучшения читаемости. Символ есть в следующем блоке кода.

else:
            for player in range(players):
                # Игроки проверяются на 21
                if set(player_hands[player]) == blackjack:
                    curr_player_results[0,player] = 1
                else:
                    # Игроки случайным образом, проверяются на перебор
                    while (random.random() >= 0.5) and (total_up(player_hands[player]) != 21):
                        player_hands[player].append(dealer_cards.pop(0))
                        if total_up(player_hands[player]) > 21:
                            curr_player_results[0,player] = -1
                            break

В финальном разделе цикла очередь дилера. Он должен брать карты до тех пор, пока не получит перебор или не наберет как минимум 17. Так что пока дилер получает карты общей суммой до 17 нужно лишь проверять, не перебор ли у него. Если он взял больше 21, тогда каждый игрок без перебора побеждает и получает 1 в curr_player_results.

# Дилер добирает карты, если нужно
        while total_up(dealer_hand) < 17:
            dealer_hand.append(dealer_cards.pop(0))
        # Сравнение очков дилера с очками игрока, но сначала проверка, не перебрал ли дилер
        if total_up(dealer_hand) > 21:
            for player in range(players):
                if curr_player_results[0,player] != -1:
                    curr_player_results[0,player] = 1

Если у дилера не перебор, тогда каждый игрок сравнивает свои карты с картами дилера — более высокое значение побеждает.

else:
            for player in range(players):
                if total_up(player_hands[player]) > total_up(dealer_hand):
                    if total_up(player_hands[player]) <= 21:
                        curr_player_results[0,player] = 1
                elif total_up(player_hands[player]) == total_up(dealer_hand):
                    curr_player_results[0,player] = 0
                else:
                    curr_player_results[0,player] = -1

В итоге результаты игры с остальными переменными добавляются в списки, которые используются для отслеживания общих результатов симуляции:

# Отслеживание результатов симуляции
        dealer_card_feature.append(dealer_hand[0])
        player_card_feature.append(player_hands)
        player_results.append(list(curr_player_results[0]))

Результаты симуляции

Теперь можно изучить результаты. Симуляция была проведена для 50 000 стеков. Вот что получилось в итоге:

• Сыграно 312 459 партий в блэкджек
• Игрок проиграл в 199 403 играх (64% всех случаев)
• Игрок победил в 99 324 играх (32% всех случаев)
• Ничья в 13 732 играх (4% всех случаев)

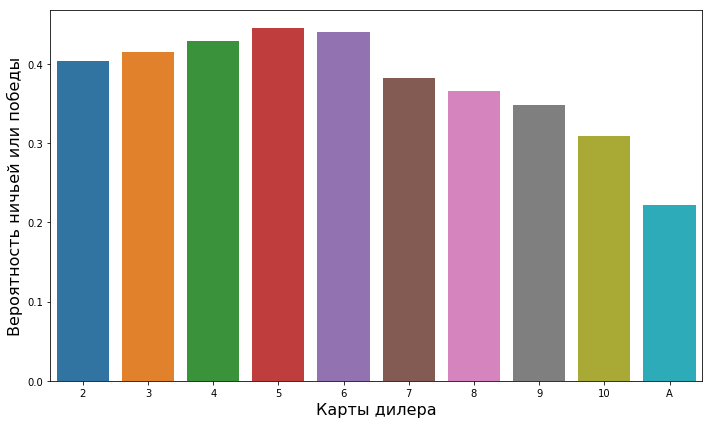
Можно взглянуть на то, как меняется вероятность выигрыша/ничьей (вероятность не проиграть деньги казино) от ключевых наблюдаемых факторов. Например, вот вероятность победы/ничьей для всех возможных карт дилера (стоит напомнить, что игроки могут видеть только одну из них):

Вероятность выигрыша или ничьей к показанной карты дилера

При наличии у дилера карты от 2 до 6 вероятность победы/ничьей увеличивается. Но после 6 она резко падает. Почему так происходит?

• Если дилер показывает карту с маленьким значением, тогда при прочих равных вполне вероятно, что у него невысокая общая сумма. В таком случае игроку проще одержать победу. Это частично объясняет, почему вероятности от 2 до 6 в среднем выше, чем от 7 до туза.
• Также нужно напомнить правило дилера — если общее значение у него в руке меньше 17, он должен брать еще карту. В этом случае увеличивается вероятность того, что у него будет перебор. Это объясняет, почему вероятность растет от 2 до 6. Подумайте, какое значение самое распространенное в колоде? Конечно, 10, ведь так оценены аж 16 из 52 карт (валеты, дамы и короли). Так что если дилер показывает 6 (при условии что мы не считаем карты) наиболее вероятное предсказание — что у него на руках 16 очков. 16 меньше 17, поэтому он вынужден брать еще. А в колоде достаточно много карт, которые приведут к тому, что у дилера будет перебор: от 6 и выше. То же касается и 5, только здесь на одну карту меньше, которая приведет к перебору (7 или выше).
• Теперь подумайте о том, что происходит, когда дилер показывает 7. В этом случае велики шансы, что у него 10. Тогда игроки с 16 очками или меньше будут вынуждены брать еще. В таком случае высока вероятность перебора. В противном — недобрать достаточно очков.

Это, если обобщить, и является главным преимуществом казино перед игроками в блэкджек — скрывая одну из карт дилера (и заставляя игроков принимать решение раньше него) они заставляют игроков предполагать худший расклад и рисковать перебором (а риск значителен).

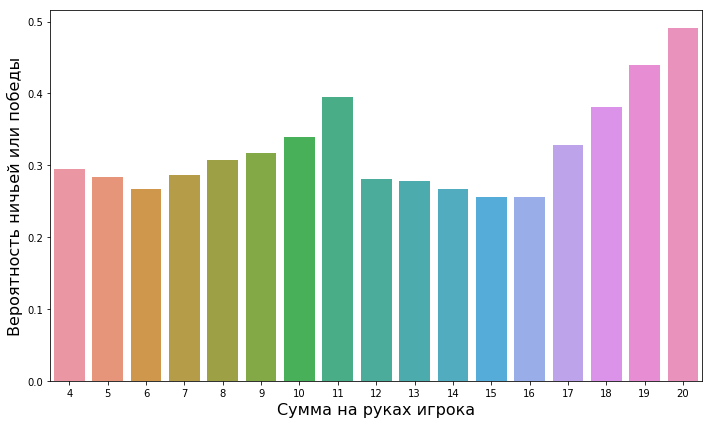
Поэтому если вы в казино и у вас на руках значение между 12 и 16, удачи, потому что шансы против вас. Теперь посмотрим на то, как начальное значение на руках у игрока (его двух стартовых карт) влияет на вероятность победы/ничьей:

Вероятность выигрыша или ничьей к сумме карт игрока

Как и следовало ожидать, вероятность победы/ничьей самая низкая для значений на руках у игрока между 12 и 16. Именно с таким количеством очков он оказывается перед ситуацией: «если я спасую, то не доберу, а если возьму еще — будет перебор». Есть смысл и в том, что 4 или 5 очков дают невысокую вероятность. Если у вас такое низкое значение и вы берете новую карту, то с большой долей вероятности на руках образуется 15, а это возвращает к ранее описанной дилемме.

Доработка алгоритма

Теперь попробуем разобраться, как с помощью простейшего эвристического алгоритма повысить шансы. Вспомните два момента:

• Основная проблема — необходимость делать ход первым (что создает риск получить перебор до дилера). Стратегия казино в том, чтобы заставить игроков действовать в условиях неопределенности в надежде на то, что они возьмут карту и получат перебор.
• Игрок в симуляторе принимает решение на основе броска монетки вне зависимости от руки (только если у него не выпало сразу 21). Поэтому даже при наличии 20 очков, есть вероятность в 50%, что он возьмет еще карту.

Попробуем увеличить шансы, сделав так, чтобы симулятор решал, брать ли новую карту только в случае нулевой вероятности перебора. Вместо броска монетки будем проверять, чтобы значение было 11 или меньше. Это не оптимальная, но простая стратегия. И поскольку она препятствует возможному перебору, то снижает риск перебора до дилера.

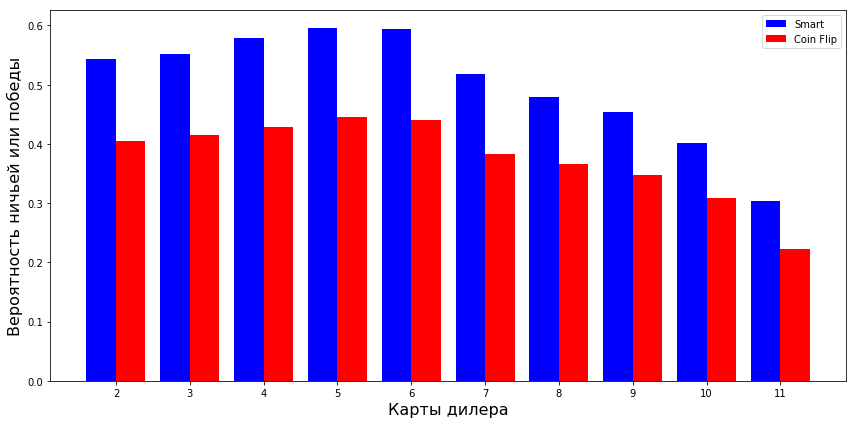
Следующий график сравнивает новую «умную» стратегию (синий цвет) с оригинальной (красный):

весь код в этом ноутбуке

Простейшее решение не рисковать, чтобы не получить перебор, значительно увеличивает шансы на победу. Тенденция никуда не делась, но увеличились шансы не потерять деньги.

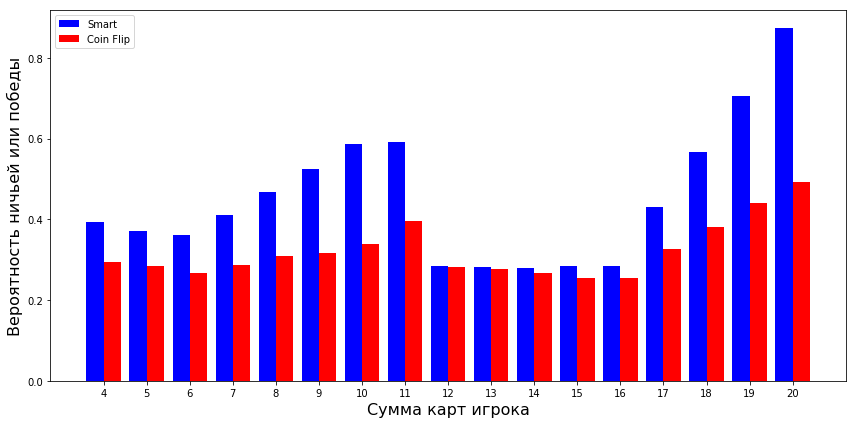
А теперь стоит взглянуть, как новая стратегия влияет на шансы на основе собственной руки:

Шансы на победу значительно увеличились для всех ситуаций кроме значений от 12 до 16. Вероятности с этими руками почти не изменились, потому что решая остаться (и не набрать перебор) игрок увеличивает вероятность того, что дилер наберет больше (ведь он останавливается как минимум с 17 очками).

Но для остальных ситуаций новая стратегия работает прекрасно.

Понравилось? Читайте вторую часть: Учим нейронную сеть играть в блэкджек

И еще раз — никогда не ставьте то, что не готовы потерять!