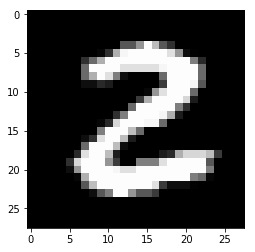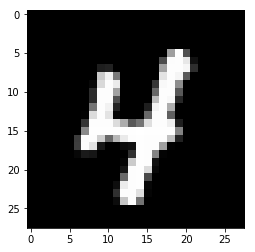Что такое машинное обучение и почему это важно?
Машинное обучение — это область искусственного интеллекта, использующая статистические методы, чтобы предоставить компьютерным системам способность «учиться». То есть постепенно улучшать производительность в конкретной задаче, с помощью данных без явного программирования. Хороший пример — то, насколько эффективно (или не очень) Gmail распознает спам или насколько совершеннее стали системы распознавания голоса с приходом Siri, Alex и Google Home.
С помощью машинного обучения решаются следующие задачи:
- Распознавание мошенничества — отслеживание необычных шаблонов в транзакциях кредитных карт или банковских счетов
- Предсказание — предсказание будущей цены акций, курса обмена валюты или криптовалюты
- Распознавание изображений — определение объектов и лиц на картинках
Машинное обучение — огромная область, и сегодня речь пойдет лишь об одной из ее составляющих.
Обучение с учителем
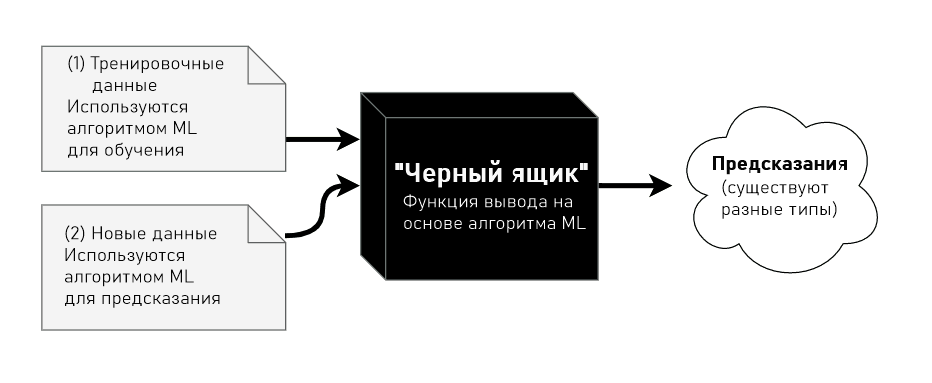
Обучение с учителем — один из видов машинного обучения. Его идея заключается в том, что систему сначала учат понимать прошлые данные, предлагая много примеров конкретной проблемы и желаемый вывод. Затем, когда система «натренирована», ей можно давать новые входные данные для предсказания выводов.
Например, как создать спам-детектор? Один из способов — интуиция. Можно вручную определять правила: например «содержит слово деньги» или «включает фразу Western Union». И пусть иногда такие системы работают, в большинстве случаев все-таки сложно создать или определить шаблоны, опираясь исключительно на интуицию.
С помощью обучения с учителем можно тренировать системы изучать лежащие в основе правила и шаблоны за счет предоставления примеров с большим количеством спама. Когда такой детектор натренирован, ему можно дать новое письмо, чтобы он попытался предсказать, является ли оно спамом.
Обучение с учителем можно использовать для предсказания вывода. Есть два типа проблем, которые решаются с его помощью: регрессия и классификация.
- В регрессионных проблемах мы пытаемся предсказать непрерывный вывод. Например, предсказание цены дома на основе данных о его размере
- В классификационных — предсказываем дискретное число качественных меток. Например, попытка предсказать, является ли письмо спамом на основе количества слов в нем.
Невозможно говорить о машинном обучении с учителем, не затронув модели обучения с учителем. Это как говорить о программировании, не касаясь языков программирования или структур данных. Модели обучения — это те самые структуры, что поддаются тренировке. Их вес (или структура) меняется по мере того, как они формируют понимание того, что нужно предсказывать. Есть несколько видов моделей обучения, например:
- Случайный лес (random forest)
- Наивный байесовский классификатор (naive Bayes)
- Логистическая регрессия (logistic regression)
- Метод k-ближайших соседей (k nearest neighbors)
В этом материале в качестве модели будет использоваться нейронная сеть.
Понимание работы нейронных сетей
Нейронные сети получили такое название, потому что их внутренняя структура должна имитировать человеческий мозг. Последний состоит из нейронов и синапсов, которые их соединяют. В момент стимуляции нейроны «активируют» другие с помощью электричества.
Каждый нейрон «активируется» в первую очередь за счет вычисления взвешенной суммы вводных данных и последующего результата с помощью результирующей функции. Когда нейрон активируется, он в свою очередь активирует остальные, которые выполняют похожие вычисления, вызывая цепную реакцию между всеми нейронами всех слоев.
Стоит отметить, что пусть нейронные сети и вдохновлены биологическими, сравнивать их все-таки нельзя.
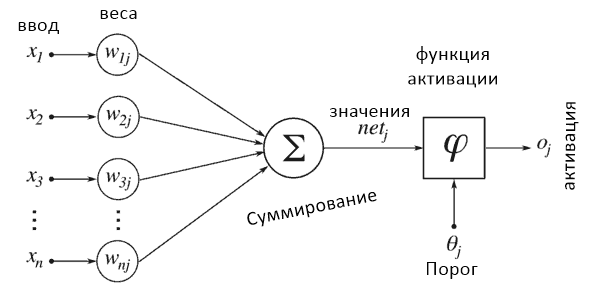
- Эта диаграмма иллюстрирует процесс активации, через который проходит каждый нейрон. Рассмотрим схему слева направо.
- Все вводные данные (числовые значения) из входящих нейронов считываются. Они определяются как x1…xn.
- Каждый ввод умножается на взвешенную сумму, ассоциированную с этим соединением. Ассоциированные веса обозначены как W1j…Wnj.
- Все взвешенные вводы суммируются и передаются активирующей функции. Она читает этот ввод и трансформирует его в числовое значение k-ближайших соседей.
- В итоге числовое значение, которое возвращает эта функция, будет вводом для другого нейрона в другом слое.
Слои нейронной сети
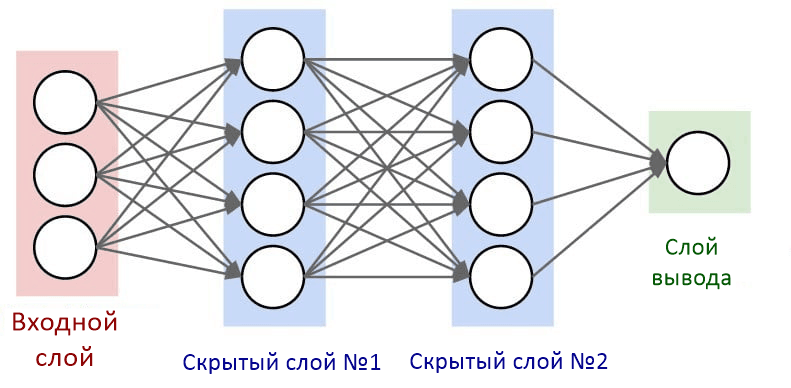
Нейроны внутри нейронной сети организованы в слои. Слои — это способ создать структуру, где каждый содержит 1 или большее количество нейронов. В нейронной сети обычно 3 или больше слоев. Также всегда определяются 2 специальных слоя, которые выполняют роль ввода и вывода.
- Слой ввода является точкой входа в нейронную сеть. В рамках программировании его можно воспринимать как аргумент функции.
- Вывод — это результат работы нейронной сети. В терминах программирования это возвращаемое функцией значение.
Слои между ними описываются как «скрытые слои». Именно там происходят все вычисления. Все слои в нейронной сети кодируются как признаковые описания.
Выбор количества скрытых слоев и нейронов
Нет золотого правила, которым стоит руководствоваться при выборе количества слоев и их размера (или числа нейронов). Как правило, стоит попробовать как минимум 1 такой слой и дальше настраивать размер, проверяя, что работает лучше всего.
Использование библиотеки Keras для тренировки простой нейронной сети, которая распознает рукописные цифры
Программистам на Python нет необходимости заново изобретать колесо. Такие библиотеки, как Tensorflow, Torch, Theano и Keras уже определили основные структуры данных для нейронной сети, оставив необходимость лишь декларативно описать структуру нейронной сети.
Keras предоставляет еще и определенную свободу: возможность выбрать количество слоев, число нейронов, тип слоя и функцию активации. На практике элементов довольно много, но в этот раз обойдемся более простыми примерами.
Как уже упоминалось, есть два специальных уровня, которые должны быть определены на основе конкретной проблемы: размер слоя ввода и размер слоя вывода. Все остальные «скрытые слои» используются для изучения сложных нелинейных абстракций задачи.
В этом материале будем использовать Python и библиотеку Keras для предсказания рукописных цифр из базы данных MNIST.
Запуск Jupyter Notebook локально
Если вы еще не работали с Jupyter Notebook, сначало изучите Руководство по Jupyter Notebook для начинающих
Список необходимых библиотек:
- numpy
- matplotlib
- sklearn
- tensorflow
Запуск из интерпретатора Python
Для запуска чистой установки Python (любой версии старше 3.6) установите требуемые модули с помощью pip.
Рекомендую (но не обязательно) запускать код в виртуальной среде.
!pip install matplotlib
!pip install sklearn
!pip install tensorflow
Если эти модули установлены, то теперь можно запускать весь код в проекте.
Импортируем модули и библиотеки:
import numpy as np
import matplotlib.pyplot as plt
import gzip
from typing import List
from sklearn.preprocessing import OneHotEncoder
import tensorflow.keras as keras
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
import itertools
%matplotlib inline
База данных MNIST
MNIST — это огромная база данных рукописных цифр, которая используется как бенчмарк и точка знакомства с машинным обучением и системами обработки изображений. Она идеально подходит, чтобы сосредоточиться именно на процессе обучения нейронной сети. MNIST — очень чистая база данных, а это роскошь в мире машинного обучения.
Цель
Натренировать систему, классифицировать каждое соответствующим ярлыком (изображенной цифрой). С помощью набора данных из 60 000 изображений рукописных цифр (представленных в виде изображений 28х28 пикселей, каждый из которых является градацией серого от 0 до 255).
Набор данных
Набор данных состоит из тренировочных и тестовых данных, но для упрощения здесь будет использоваться только тренировочный. Вот так его загрузить:
%%bash
rm -Rf train-images-idx3-ubyte.gz
rm -Rf train-labels-idx1-ubyte.gz
wget -q http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz
wget -q http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz
Чтение меток
Есть 10 цифр: (0-9), поэтому каждая метка должна быть цифрой от 0 до 9. Загруженный файл, train-labels-idx1-ubyte.gz, кодирует метки следующим образом:
Файл ярлыка тренировочного набора (train-labels-idx1-ubyte):
| [offset] | [type] | [value] | [description] |
|---|---|---|---|
| 0000 | 32 bit integer | 0x00000801(2049) | magic number (MSB first) |
| 0004 | 32 bit integer | 60000 | number of items |
| 0008 | unsigned byte | ?? | label |
| 0009 | unsigned byte | ?? | label |
| …… | …… | …… | …… |
| xxxx | unsigned byte | ?? | label |
Значения меток от 0 до 9.
Первые 8 байт (или первые 2 32-битных целых числа) можно пропустить, потому что они содержат метаданные файлы, необходимые для низкоуровневых языков программирования. Для парсинга файла нужно проделать следующие операции:
- Открыть файл с помощью библиотеки gzip, чтобы его можно было распаковать
- Прочитать весь массив байтов в память
- Пропустить первые 8 байт
- Перебирать каждый байт и приводить его к целому числу
Примечание: если этот файл из непроверенного источника, понадобится куда больше проверок. Но предположим, что этот конкретный является надежным и подходит для целей материала.
with gzip.open('train-labels-idx1-ubyte.gz') as train_labels:
data_from_train_file = train_labels.read()
# Пропускаем первые 8 байт
label_data = data_from_train_file[8:]
assert len(label_data) == 60000
# Конвертируем каждый байт в целое число.
# Это будет число от 0 до 9
labels = [int(label_byte) for label_byte in label_data]
assert min(labels) == 0 and max(labels) == 9
assert len(labels) == 60000
Чтение изображений
| [offset] | [type] | [value] | [description] |
|---|---|---|---|
| 0000 | 32 bit integer | 0x00000803(2051) | magic number |
| 0004 | 32 bit integer | 60000 | number of images |
| 0008 | 32 bit integer | 28 | number of rows |
| 0012 | 32 bit integer | 28 | number of columns |
| 0016 | unsigned byte | ?? | pixel |
| 0017 | unsigned byte | ?? | pixel |
| …… | …… | …… | …… |
| xxxx | unsigned byte | ?? | pixel |
Чтение изображений немного отличается от чтения меток. Первые 16 байт содержат уже известные метаданные. Их можно пропустить и переходить сразу к чтению изображений. Каждое из них представлено в виде массива 28*28 из байтов без знака. Все что требуется — читать по одному изображению за раз и сохранять их в массив.
SIZE_OF_ONE_IMAGE = 28 ** 2
images = []
# Перебор тренировочного файла и читение одного изображения за раз
with gzip.open('train-images-idx3-ubyte.gz') as train_images:
train_images.read(4 * 4)
ctr = 0
for _ in range(60000):
image = train_images.read(size=SIZE_OF_ONE_IMAGE)
assert len(image) == SIZE_OF_ONE_IMAGE
# Конвертировать в NumPy
image_np = np.frombuffer(image, dtype='uint8') / 255
images.append(image_np)
images = np.array(images)
images.shape
Вывод: (60000, 784)
В списке 60000 изображений. Каждое из них представлено битовым вектором размером SIZE_OF_ONE_IMAGE. Попробуем построить изображение с помощью библиотеки matplotlib:
def plot_image(pixels: np.array):
plt.imshow(pixels.reshape((28, 28)), cmap='gray')
plt.show()
plot_image(images[25])
Кодирование меток изображения с помощью One-hot encoding
Будем использовать one-hot encoding для превращения целевых меток в вектор.
labels_np = np.array(labels).reshape((-1, 1))
encoder = OneHotEncoder(categories='auto')
labels_np_onehot = encoder.fit_transform(labels_np).toarray()
labels_np_onehot
array([[0., 0., 0., ..., 0., 0., 0.],
[1., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 1., 0.]])
Были успешно созданы входные данные и векторный вывод, который будет поступать на входной и выходной слои нейронной сети. Вектор ввода с индексом i будет отвечать вектору вывода с индексом i.
Вводные данные:
labels_np_onehot[999]
Вывод:
array([0., 0., 0., 0., 0., 0., 1., 0., 0., 0.])
Вводные данные:
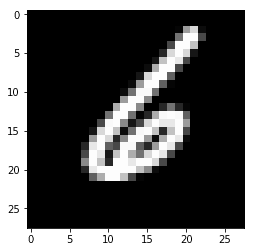
plot_image(images[999])
Вывод:
В примере выше явно видно, что изображение с индексом 999 представляет цифру 6. Ассоциированный с ним вектор содержит 10 цифр (поскольку имеется 10 меток), а цифра с индексом 6 равно 1. Это значит, что метка правильная.
Разделение датасета на тренировочный и тестовый
Для проверки того, что нейронная сеть была натренирована правильно, берем определенный процент тренировочного набора (60 000 изображений) и используем его в тестовых целях.
Вводные данные:
X_train, X_test, y_train, y_test = train_test_split(images, labels_np_onehot)
print(y_train.shape)
print(y_test.shape)
(45000, 10)
(15000, 10)
Здесь видно, что весь набор из 60 000 изображений бал разбит на два: один с 45 000, а другой с 15 000 изображений.
Тренировка нейронной сети с помощью Keras
model = keras.Sequential()
model.add(keras.layers.Dense(input_shape=(SIZE_OF_ONE_IMAGE,), units=128, activation='relu'))
model.add(keras.layers.Dense(10, activation='softmax'))
model.summary()
model.compile(optimizer='sgd',
loss='categorical_crossentropy',
metrics=['accuracy'])
Вывод:
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 128) 100480
_________________________________________________________________
dense_1 (Dense) (None, 10) 1290
=================================================================
Total params: 101,770
Trainable params: 101,770
Non-trainable params: 0
_________________________________________________________________
Для обучения нейронной сети, выполним этот код.
model.fit(X_train, y_train, epochs=20, batch_size=128)
Вывод:
Train on 45000 samples
Epoch 1/20
45000/45000 [==============================] - 2s 54us/sample - loss: 1.3391 - accuracy: 0.6710
Epoch 2/20
45000/45000 [==============================] - 2s 39us/sample - loss: 0.6489 - accuracy: 0.8454
...
Epoch 20/20
45000/45000 [==============================] - 2s 40us/sample - loss: 0.2584 - accuracy: 0.9279
Проверяем точность на тренировочных данных.
model.evaluate(X_test, y_test)
Вывод:
[0.2567395991722743, 0.9264]
Посмотрим результаты
Вот вы и натренировали нейронную сеть для предсказания рукописных цифры с точностью выше 90%. Проверим ее с помощью изображения из тестового набора.
Возьмем случайное изображение — картинку с индексом 1010. Берем предсказанную метку (в данном случае — 4, потому что на пятой позиции стоит цифра 1)
y_test[1010]
Вывод:
array([0., 0., 0., 0., 1., 0., 0., 0., 0., 0.])
Построим изображения соответствующей картинки
plot_image(X_test[1010])
Понимание вывода активационного слоя softmax
Пропустим цифру через нейронную сеть и посмотрим, какой вывод она предскажет.
Вводные данные:
predicted_results = model.predict(X_test[1010].reshape((1, -1)))
Вывод слоя softmax — это распределение вероятностей для каждого вывода. В этом случае их может быть 10 (цифры от 0 до 9). Но ожидается, что каждое изображение будет соответствовать лишь одному.
Поскольку это распределение вероятностей, их сумма приблизительно равна 1 (единице).
predicted_results.sum()
1.0000001
Чтение вывода слоя softmax для конкретной цифры
Как можно видеть дальше, 5-ой индекс действительно близок к 1 (0,99), а это значит, что он с большой долей вероятности является
4… а это так и есть!
predicted_results
array([[1.2202066e-06, 3.4432333e-08, 3.5151488e-06, 1.2011528e-06, 9.9889344e-01, 3.5855610e-05, 1.6140550e-05, 7.6822333e-05, 1.0446112e-04, 8.6736667e-04]], dtype=float32)
Просмотр матрицы ошибок
predicted_outputs = np.argmax(model.predict(X_test), axis=1)
expected_outputs = np.argmax(y_test, axis=1)
predicted_confusion_matrix = confusion_matrix(expected_outputs, predicted_outputs)
predicted_confusion_matrix
array([[1402, 0, 4, 3, 1, 6, 20, 2, 21, 2],
[ 1, 1684, 9, 5, 4, 9, 1, 3, 9, 3],
[ 13, 8, 1280, 9, 19, 5, 12, 15, 17, 8],
[ 6, 8, 37, 1404, 1, 53, 3, 17, 33, 15],
[ 4, 7, 8, 0, 1345, 1, 18, 3, 8, 54],
[ 17, 8, 9, 31, 25, 1157, 25, 3, 24, 12],
[ 9, 6, 10, 0, 10, 12, 1431, 0, 6, 1],
[ 3, 11, 17, 4, 23, 2, 1, 1484, 5, 40],
[ 11, 16, 24, 40, 9, 25, 13, 3, 1348, 25],
[ 5, 5, 6, 16, 31, 6, 0, 43, 7, 1381]],
dtype=int64)
# это код из https://scikit-learn.org/stable/auto_examples/model_selection/plot_confusion_matrix.html
def plot_confusion_matrix(cm, classes,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.tight_layout()
# Compute confusion matrix
class_names = [str(idx) for idx in range(10)]
cnf_matrix = confusion_matrix(expected_outputs, predicted_outputs)
np.set_printoptions(precision=2)
# Plot non-normalized confusion matrix
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=class_names,
title='Confusion matrix, without normalization')
plt.show()
Выводы
В течение этого руководства вы должны были разобраться с основными концепциями, которые составляют основу машинного обучения, а также научиться:
- Кодировать и декодировать изображения в наборе данных MNIST
- Кодировать категориальные значения с помощью “one-hot encoding”
- Определять нейронную сеть с двумя скрытыми слоями, а также слой вывода, использующий функцию активации softmax
- Изучать результаты вывода функции активации softmax
- Строить матрицу ошибок классификатора
Библиотеки Sci-Kit Learn и Keras значительно понизили порог входа в машинное обучение — так же, как Python снизил порог знакомства с программированием. Однако потребуются годы (или десятилетия), чтобы достичь экспертного уровня!
Программисты, обладающие навыками машинного обучения, очень востребованы. С помощью упомянутых библиотек и вводных материалов о практических аспектах машинного обучения у всех должна быть возможность познакомиться с этой областью знаний. Даже если теоретических знаний о модели, библиотеке или фреймворке нет.
Затем навыки нужно использовать на практике, разрабатывая более умные продукты, что сделает потребителей более вовлеченными.
Попробуйте сами
Вот что вы можете попробовать сделать сами, чтобы углубиться в мир машинного обучения с Python:
- Поэкспериментируйте с количеством нейронов в скрытом слое. Сможете ли вы увеличить точность?
- Попробуйте добавить больше слоев. Тренируется ли сеть от этого медленнее? Понимаете ли вы, почему?
- Попробуйте RandomForestClassifier (нужна библиотека scikit-learn) вместо нейронной сети. Увеличилась ли точность?